Plug-and-Play Regularization using Linear Solvers
Paper and Code
Sep 16, 2022


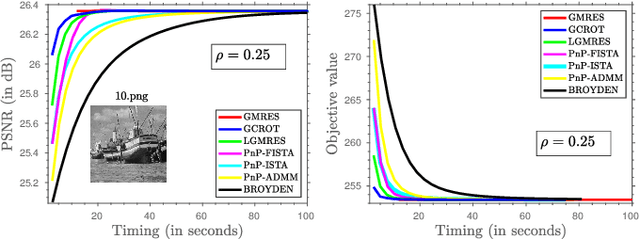
There has been tremendous research on the design of image regularizers over the years, from simple Tikhonov and Laplacian to sophisticated sparsity and CNN-based regularizers. Coupled with a model-based loss function, these are typically used for image reconstruction within an optimization framework. The technical challenge is to develop a regularizer that can accurately model realistic images and be optimized efficiently along with the loss function. Motivated by the recent plug-and-play paradigm for image regularization, we construct a quadratic regularizer whose reconstruction capability is competitive with state-of-the-art regularizers. The novelty of the regularizer is that, unlike classical regularizers, the quadratic objective function is derived from the observed data. Since the regularizer is quadratic, we can reduce the optimization to solving a linear system for applications such as superresolution, deblurring, inpainting, etc. In particular, we show that using iterative Krylov solvers, we can converge to the solution in a few iterations, where each iteration requires an application of the forward operator and a linear denoiser. The surprising finding is that we can get close to deep learning methods in terms of reconstruction quality. To the best of our knowledge, the possibility of achieving near state-of-the-art performance using a linear solver is novel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge