Kunal. N. Chaudhury
Fast High-Dimensional Bilateral and Nonlocal Means Filtering
Nov 06, 2018


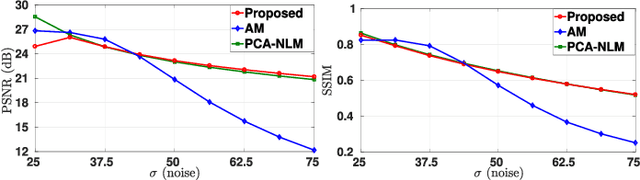
Abstract:Existing fast algorithms for bilateral and nonlocal means filtering mostly work with grayscale images. They cannot easily be extended to high-dimensional data such as color and hyperspectral images, patch-based data, flow-fields, etc. In this paper, we propose a fast algorithm for high-dimensional bilateral and nonlocal means filtering. Unlike existing approaches, where the focus is on approximating the data (using quantization) or the filter kernel (via analytic expansions), we locally approximate the kernel using weighted and shifted copies of a Gaussian, where the weights and shifts are inferred from the data. The algorithm emerging from the proposed approximation essentially involves clustering and fast convolutions, and is easy to implement. Moreover, a variant of our algorithm comes with a guarantee (bound) on the approximation error, which is not enjoyed by existing algorithms. We present some results for high-dimensional bilateral and nonlocal means filtering to demonstrate the speed and accuracy of our proposal. Moreover, we also show that our algorithm can outperform state-of-the-art fast approximations in terms of accuracy and timing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge