Plug-and-Play Compressed Sensing: Theoretical Guarantees on Exact and Robust Recovery

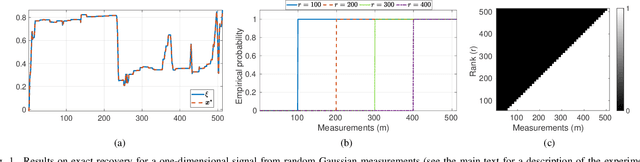
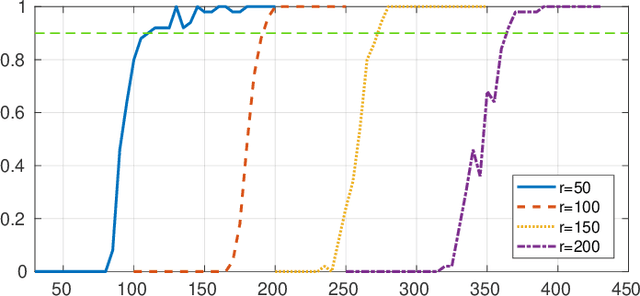
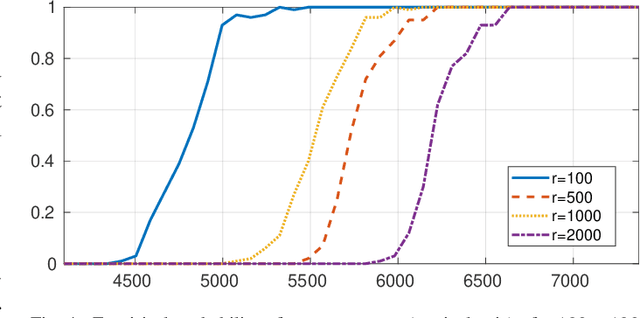
In Plug-and-Play (PnP) algorithms, an off-the-shelf denoiser is used for image regularization. PnP yields state-of-the-art results, but its theoretical aspects are not well understood. This work considers the question: Similar to classical compressed sensing (CS), can we theoretically recover the ground-truth via PnP under suitable conditions on the denoiser and the sensing matrix? One hurdle is that since PnP is an algorithmic framework, its solution need not be the minimizer of some objective function. It was recently shown that a convex regularizer $\Phi$ can be associated with a class of linear denoisers such that PnP amounts to solving a convex problem involving $\Phi$. Motivated by this, we consider the PnP analog of CS: minimize $\Phi(x)$ s.t. $Ax=A\xi$, where $A$ is a $m\times n$ random sensing matrix, $\Phi$ is the regularizer associated with a linear denoiser $W$, and $\xi$ is the ground-truth. We prove that if $A$ is Gaussian and $\xi$ is in the range of $W$, then the minimizer is almost surely $\xi$ if $rank(W)\leq m$, and almost never if $rank(W)> m$. Thus, the range of the PnP denoiser acts as a signal prior, and its dimension marks a sharp transition from failure to success of exact recovery. We extend the result to subgaussian sensing matrices, except that exact recovery holds only with high probability. For noisy measurements $b = A \xi + \eta$, we consider a robust formulation: minimize $\Phi(x)$ s.t. $\|Ax-b\|\leq\delta$. We prove that for an optimal solution $x^*$, with high probability the distortion $\|x^*-\xi\|$ is bounded by $\|\eta\|$ and $\delta$ if the number of measurements is large enough. In particular, we can derive the sample complexity of CS as a function of distortion error and success rate. We discuss the extension of these results to random Fourier measurements, perform numerical experiments, and discuss research directions stemming from this work.