Linear Convergence of Plug-and-Play Algorithms with Kernel Denoisers

The use of denoisers for image reconstruction has shown significant potential, especially for the Plug-and-Play (PnP) framework. In PnP, a powerful denoiser is used as an implicit regularizer in proximal algorithms such as ISTA and ADMM. The focus of this work is on the convergence of PnP iterates for linear inverse problems using kernel denoisers. It was shown in prior work that the update operator in standard PnP is contractive for symmetric kernel denoisers under appropriate conditions on the denoiser and the linear forward operator. Consequently, we could establish global linear convergence of the iterates using the contraction mapping theorem. In this work, we develop a unified framework to establish global linear convergence for symmetric and nonsymmetric kernel denoisers. Additionally, we derive quantitative bounds on the contraction factor (convergence rate) for inpainting, deblurring, and superresolution. We present numerical results to validate our theoretical findings.

On the Contractivity of Plug-and-Play Operators

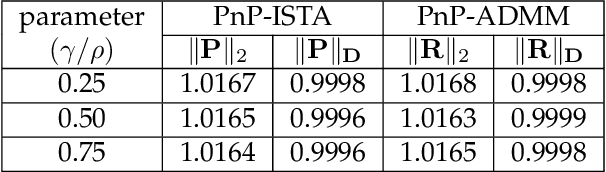
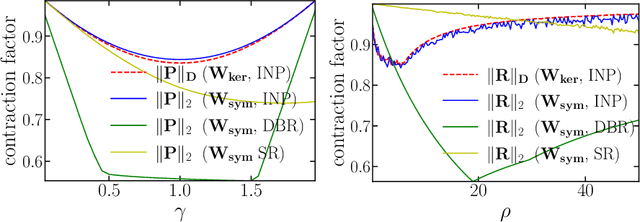
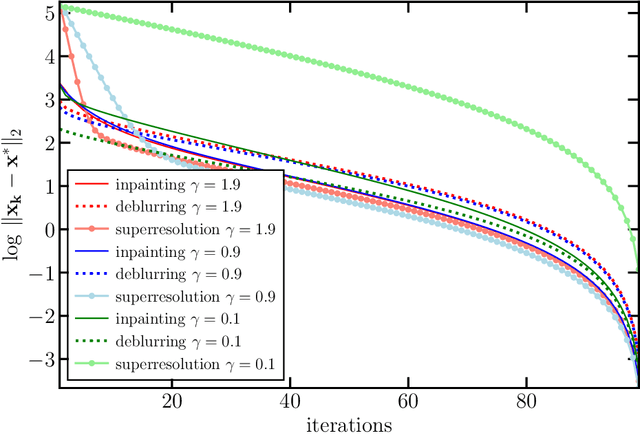
In plug-and-play (PnP) regularization, the proximal operator in algorithms such as ISTA and ADMM is replaced by a powerful denoiser. This formal substitution works surprisingly well in practice. In fact, PnP has been shown to give state-of-the-art results for various imaging applications. The empirical success of PnP has motivated researchers to understand its theoretical underpinnings and, in particular, its convergence. It was shown in prior work that for kernel denoisers such as the nonlocal means, PnP-ISTA provably converges under some strong assumptions on the forward model. The present work is motivated by the following questions: Can we relax the assumptions on the forward model? Can the convergence analysis be extended to PnP-ADMM? Can we estimate the convergence rate? In this letter, we resolve these questions using the contraction mapping theorem: (i) for symmetric denoisers, we show that (under mild conditions) PnP-ISTA and PnP-ADMM exhibit linear convergence; and (ii) for kernel denoisers, we show that PnP-ISTA and PnP-ADMM converge linearly for image inpainting. We validate our theoretical findings using reconstruction experiments.

Plug-and-Play Compressed Sensing: Theoretical Guarantees on Exact and Robust Recovery

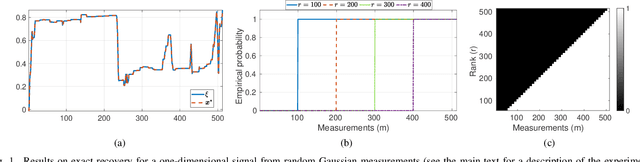
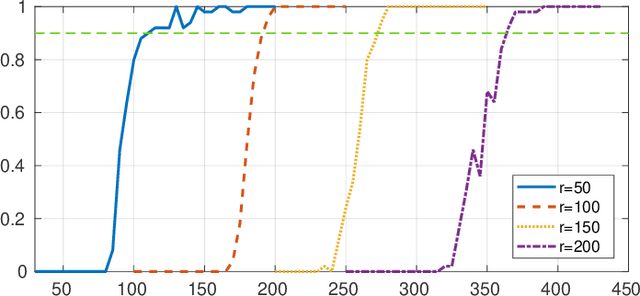
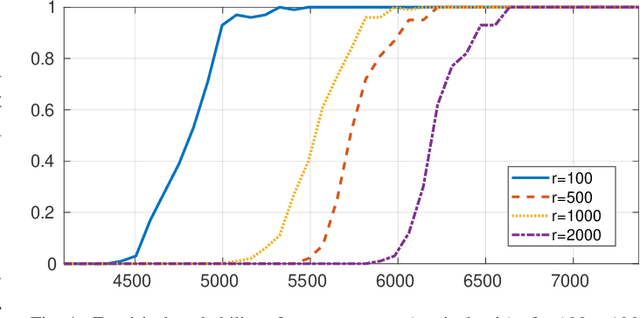
In Plug-and-Play (PnP) algorithms, an off-the-shelf denoiser is used for image regularization. PnP yields state-of-the-art results, but its theoretical aspects are not well understood. This work considers the question: Similar to classical compressed sensing (CS), can we theoretically recover the ground-truth via PnP under suitable conditions on the denoiser and the sensing matrix? One hurdle is that since PnP is an algorithmic framework, its solution need not be the minimizer of some objective function. It was recently shown that a convex regularizer $\Phi$ can be associated with a class of linear denoisers such that PnP amounts to solving a convex problem involving $\Phi$. Motivated by this, we consider the PnP analog of CS: minimize $\Phi(x)$ s.t. $Ax=A\xi$, where $A$ is a $m\times n$ random sensing matrix, $\Phi$ is the regularizer associated with a linear denoiser $W$, and $\xi$ is the ground-truth. We prove that if $A$ is Gaussian and $\xi$ is in the range of $W$, then the minimizer is almost surely $\xi$ if $rank(W)\leq m$, and almost never if $rank(W)> m$. Thus, the range of the PnP denoiser acts as a signal prior, and its dimension marks a sharp transition from failure to success of exact recovery. We extend the result to subgaussian sensing matrices, except that exact recovery holds only with high probability. For noisy measurements $b = A \xi + \eta$, we consider a robust formulation: minimize $\Phi(x)$ s.t. $\|Ax-b\|\leq\delta$. We prove that for an optimal solution $x^*$, with high probability the distortion $\|x^*-\xi\|$ is bounded by $\|\eta\|$ and $\delta$ if the number of measurements is large enough. In particular, we can derive the sample complexity of CS as a function of distortion error and success rate. We discuss the extension of these results to random Fourier measurements, perform numerical experiments, and discuss research directions stemming from this work.

On Plug-and-Play Regularization using Linear Denoisers

In plug-and-play (PnP) regularization, the knowledge of the forward model is combined with a powerful denoiser to obtain state-of-the-art image reconstructions. This is typically done by taking a proximal algorithm such as FISTA or ADMM, and formally replacing the proximal map associated with a regularizer by nonlocal means, BM3D or a CNN denoiser. Each iterate of the resulting PnP algorithm involves some kind of inversion of the forward model followed by denoiser-induced regularization. A natural question in this regard is that of optimality, namely, do the PnP iterations minimize some f+g, where f is a loss function associated with the forward model and g is a regularizer? This has a straightforward solution if the denoiser can be expressed as a proximal map, as was shown to be the case for a class of linear symmetric denoisers. However, this result excludes kernel denoisers such as nonlocal means that are inherently non-symmetric. In this paper, we prove that a broader class of linear denoisers (including symmetric denoisers and kernel denoisers) can be expressed as a proximal map of some convex regularizer g. An algorithmic implication of this result for non-symmetric denoisers is that it necessitates appropriate modifications in the PnP updates to ensure convergence to a minimum of f+g. Apart from the convergence guarantee, the modified PnP algorithms are shown to produce good restorations.