Linear Convergence of Plug-and-Play Algorithms with Kernel Denoisers

The use of denoisers for image reconstruction has shown significant potential, especially for the Plug-and-Play (PnP) framework. In PnP, a powerful denoiser is used as an implicit regularizer in proximal algorithms such as ISTA and ADMM. The focus of this work is on the convergence of PnP iterates for linear inverse problems using kernel denoisers. It was shown in prior work that the update operator in standard PnP is contractive for symmetric kernel denoisers under appropriate conditions on the denoiser and the linear forward operator. Consequently, we could establish global linear convergence of the iterates using the contraction mapping theorem. In this work, we develop a unified framework to establish global linear convergence for symmetric and nonsymmetric kernel denoisers. Additionally, we derive quantitative bounds on the contraction factor (convergence rate) for inpainting, deblurring, and superresolution. We present numerical results to validate our theoretical findings.

FISTA Iterates Converge Linearly for Denoiser-Driven Regularization

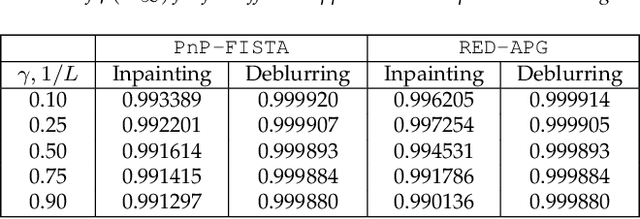
The effectiveness of denoising-driven regularization for image reconstruction has been widely recognized. Two prominent algorithms in this area are Plug-and-Play ($\texttt{PnP}$) and Regularization-by-Denoising ($\texttt{RED}$). We consider two specific algorithms $\texttt{PnP-FISTA}$ and $\texttt{RED-APG}$, where regularization is performed by replacing the proximal operator in the $\texttt{FISTA}$ algorithm with a powerful denoiser. The iterate convergence of $\texttt{FISTA}$ is known to be challenging with no universal guarantees. Yet, we show that for linear inverse problems and a class of linear denoisers, global linear convergence of the iterates of $\texttt{PnP-FISTA}$ and $\texttt{RED-APG}$ can be established through simple spectral analysis.

On the Strong Convexity of PnP Regularization Using Linear Denoisers

In the Plug-and-Play (PnP) method, a denoiser is used as a regularizer within classical proximal algorithms for image reconstruction. It is known that a broad class of linear denoisers can be expressed as the proximal operator of a convex regularizer. Consequently, the associated PnP algorithm can be linked to a convex optimization problem $\mathcal{P}$. For such a linear denoiser, we prove that $\mathcal{P}$ exhibits strong convexity for linear inverse problems. Specifically, we show that the strong convexity of $\mathcal{P}$ can be used to certify objective and iterative convergence of any PnP algorithm derived from classical proximal methods.