FISTA Iterates Converge Linearly for Denoiser-Driven Regularization
Paper and Code
Nov 16, 2024
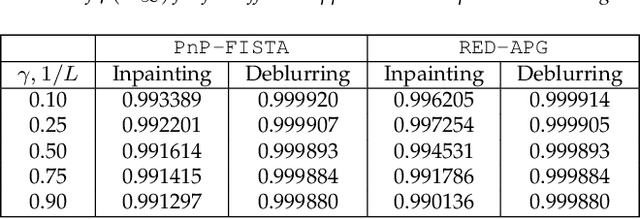


The effectiveness of denoising-driven regularization for image reconstruction has been widely recognized. Two prominent algorithms in this area are Plug-and-Play ($\texttt{PnP}$) and Regularization-by-Denoising ($\texttt{RED}$). We consider two specific algorithms $\texttt{PnP-FISTA}$ and $\texttt{RED-APG}$, where regularization is performed by replacing the proximal operator in the $\texttt{FISTA}$ algorithm with a powerful denoiser. The iterate convergence of $\texttt{FISTA}$ is known to be challenging with no universal guarantees. Yet, we show that for linear inverse problems and a class of linear denoisers, global linear convergence of the iterates of $\texttt{PnP-FISTA}$ and $\texttt{RED-APG}$ can be established through simple spectral analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge