Temperature Balancing, Layer-wise Weight Analysis, and Neural Network Training

Regularization in modern machine learning is crucial, and it can take various forms in algorithmic design: training set, model family, error function, regularization terms, and optimizations. In particular, the learning rate, which can be interpreted as a temperature-like parameter within the statistical mechanics of learning, plays a crucial role in neural network training. Indeed, many widely adopted training strategies basically just define the decay of the learning rate over time. This process can be interpreted as decreasing a temperature, using either a global learning rate (for the entire model) or a learning rate that varies for each parameter. This paper proposes TempBalance, a straightforward yet effective layer-wise learning rate method. TempBalance is based on Heavy-Tailed Self-Regularization (HT-SR) Theory, an approach which characterizes the implicit self-regularization of different layers in trained models. We demonstrate the efficacy of using HT-SR-motivated metrics to guide the scheduling and balancing of temperature across all network layers during model training, resulting in improved performance during testing. We implement TempBalance on CIFAR10, CIFAR100, SVHN, and TinyImageNet datasets using ResNets, VGGs, and WideResNets with various depths and widths. Our results show that TempBalance significantly outperforms ordinary SGD and carefully-tuned spectral norm regularization. We also show that TempBalance outperforms a number of state-of-the-art optimizers and learning rate schedulers.

PCL-Indexability and Whittle Index for Restless Bandits with General Observation Models

In this paper, we consider a general observation model for restless multi-armed bandit problems. The operation of the player needs to be based on certain feedback mechanism that is error-prone due to resource constraints or environmental or intrinsic noises. By establishing a general probabilistic model for dynamics of feedback/observation, we formulate the problem as a restless bandit with a countable belief state space starting from an arbitrary initial belief (a priori information). We apply the achievable region method with partial conservation law (PCL) to the infinite-state problem and analyze its indexability and priority index (Whittle index). Finally, we propose an approximation process to transform the problem into which the AG algorithm of Ni\~no-Mora and Bertsimas for finite-state problems can be applied to. Numerical experiments show that our algorithm has an excellent performance.

Whittle Index for A Class of Restless Bandits with Imperfect Observations

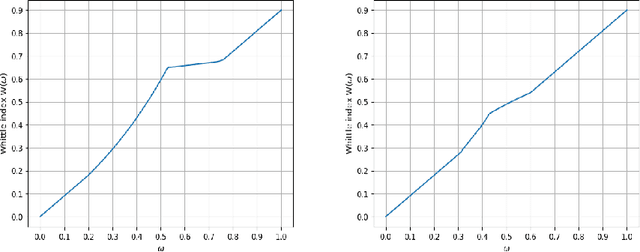
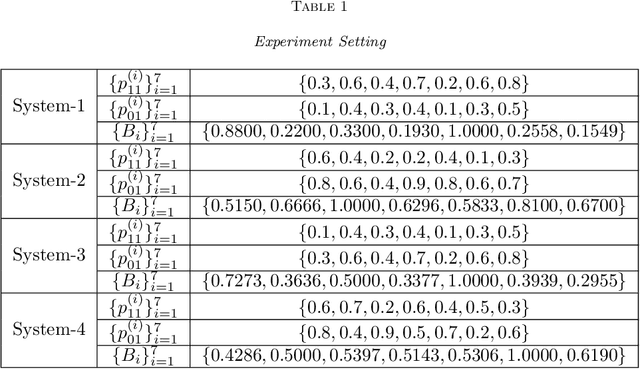
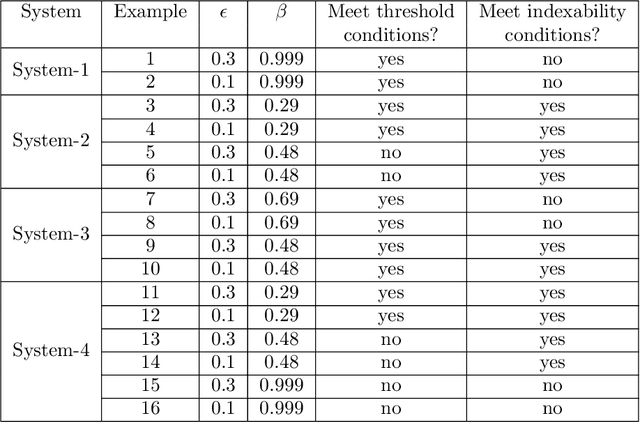
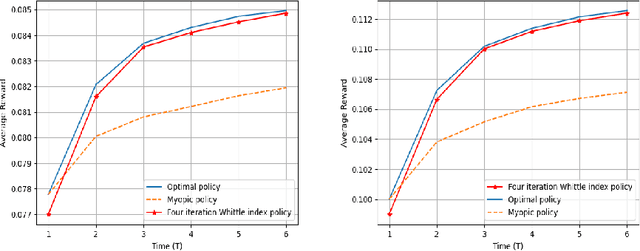
We consider a class of restless bandit problems that finds a broad application area in stochastic optimization, reinforcement learning and operations research. In our model, there are $N$ independent $2$-state Markov processes that may be observed and accessed for accruing rewards. The observation is error-prone, i.e., both false alarm and miss detection may happen. Furthermore, the user can only choose a subset of $M~(M<N)$ processes to observe at each discrete time. If a process in state~$1$ is correctly observed, then it will offer some reward. Due to the partial and imperfect observation model, the system is formulated as a restless multi-armed bandit problem with an information state space of uncountable cardinality. Restless bandit problems with finite state spaces are PSPACE-HARD in general. In this paper, we establish a low-complexity algorithm that achieves a strong performance for this class of restless bandits. Under certain conditions, we theoretically prove the existence (indexability) of Whittle index and its equivalence to our algorithm. When those conditions do not hold, we show by numerical experiments the near-optimal performance of our algorithm in general.

Deterministic Sequencing of Exploration and Exploitation for Multi-Armed Bandit Problems

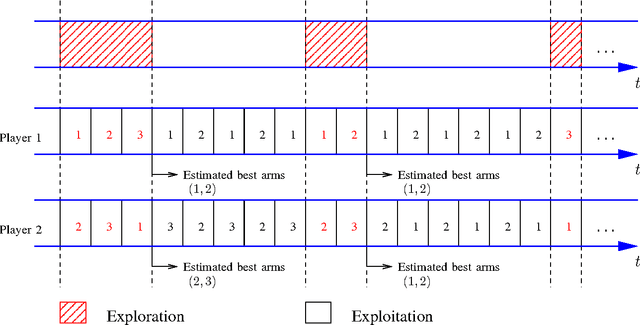
In the Multi-Armed Bandit (MAB) problem, there is a given set of arms with unknown reward models. At each time, a player selects one arm to play, aiming to maximize the total expected reward over a horizon of length T. An approach based on a Deterministic Sequencing of Exploration and Exploitation (DSEE) is developed for constructing sequential arm selection policies. It is shown that for all light-tailed reward distributions, DSEE achieves the optimal logarithmic order of the regret, where regret is defined as the total expected reward loss against the ideal case with known reward models. For heavy-tailed reward distributions, DSEE achieves O(T^1/p) regret when the moments of the reward distributions exist up to the pth order for 1<p<=2 and O(T^1/(1+p/2)) for p>2. With the knowledge of an upperbound on a finite moment of the heavy-tailed reward distributions, DSEE offers the optimal logarithmic regret order. The proposed DSEE approach complements existing work on MAB by providing corresponding results for general reward distributions. Furthermore, with a clearly defined tunable parameter-the cardinality of the exploration sequence, the DSEE approach is easily extendable to variations of MAB, including MAB with various objectives, decentralized MAB with multiple players and incomplete reward observations under collisions, MAB with unknown Markov dynamics, and combinatorial MAB with dependent arms that often arise in network optimization problems such as the shortest path, the minimum spanning, and the dominating set problems under unknown random weights.

Adaptive Shortest-Path Routing under Unknown and Stochastically Varying Link States

We consider the adaptive shortest-path routing problem in wireless networks under unknown and stochastically varying link states. In this problem, we aim to optimize the quality of communication between a source and a destination through adaptive path selection. Due to the randomness and uncertainties in the network dynamics, the quality of each link varies over time according to a stochastic process with unknown distributions. After a path is selected for communication, the aggregated quality of all links on this path (e.g., total path delay) is observed. The quality of each individual link is not observable. We formulate this problem as a multi-armed bandit with dependent arms. We show that by exploiting arm dependencies, a regret polynomial with network size can be achieved while maintaining the optimal logarithmic order with time. This is in sharp contrast with the exponential regret order with network size offered by a direct application of the classic MAB policies that ignore arm dependencies. Furthermore, our results are obtained under a general model of link-quality distributions (including heavy-tailed distributions) and find applications in cognitive radio and ad hoc networks with unknown and dynamic communication environments.

Learning in A Changing World: Restless Multi-Armed Bandit with Unknown Dynamics

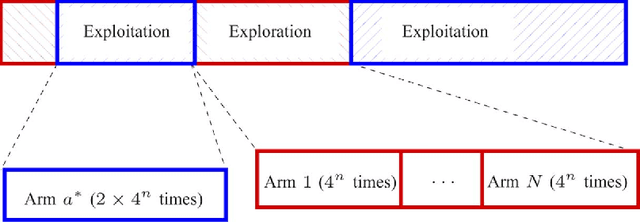
We consider the restless multi-armed bandit (RMAB) problem with unknown dynamics in which a player chooses M out of N arms to play at each time. The reward state of each arm transits according to an unknown Markovian rule when it is played and evolves according to an arbitrary unknown random process when it is passive. The performance of an arm selection policy is measured by regret, defined as the reward loss with respect to the case where the player knows which M arms are the most rewarding and always plays the M best arms. We construct a policy with an interleaving exploration and exploitation epoch structure that achieves a regret with logarithmic order when arbitrary (but nontrivial) bounds on certain system parameters are known. When no knowledge about the system is available, we show that the proposed policy achieves a regret arbitrarily close to the logarithmic order. We further extend the problem to a decentralized setting where multiple distributed players share the arms without information exchange. Under both an exogenous restless model and an endogenous restless model, we show that a decentralized extension of the proposed policy preserves the logarithmic regret order as in the centralized setting. The results apply to adaptive learning in various dynamic systems and communication networks, as well as financial investment.

Extended UCB Policy for Multi-Armed Bandit with Light-Tailed Reward Distributions

We consider the multi-armed bandit problems in which a player aims to accrue reward by sequentially playing a given set of arms with unknown reward statistics. In the classic work, policies were proposed to achieve the optimal logarithmic regret order for some special classes of light-tailed reward distributions, e.g., Auer et al.'s UCB1 index policy for reward distributions with finite support. In this paper, we extend Auer et al.'s UCB1 index policy to achieve the optimal logarithmic regret order for all light-tailed (or equivalently, locally sub-Gaussian) reward distributions defined by the (local) existence of the moment-generating function.

Decentralized Restless Bandit with Multiple Players and Unknown Dynamics

We consider decentralized restless multi-armed bandit problems with unknown dynamics and multiple players. The reward state of each arm transits according to an unknown Markovian rule when it is played and evolves according to an arbitrary unknown random process when it is passive. Players activating the same arm at the same time collide and suffer from reward loss. The objective is to maximize the long-term reward by designing a decentralized arm selection policy to address unknown reward models and collisions among players. A decentralized policy is constructed that achieves a regret with logarithmic order when an arbitrary nontrivial bound on certain system parameters is known. When no knowledge about the system is available, we extend the policy to achieve a regret arbitrarily close to the logarithmic order. The result finds applications in communication networks, financial investment, and industrial engineering.

Distributed Learning in Multi-Armed Bandit with Multiple Players

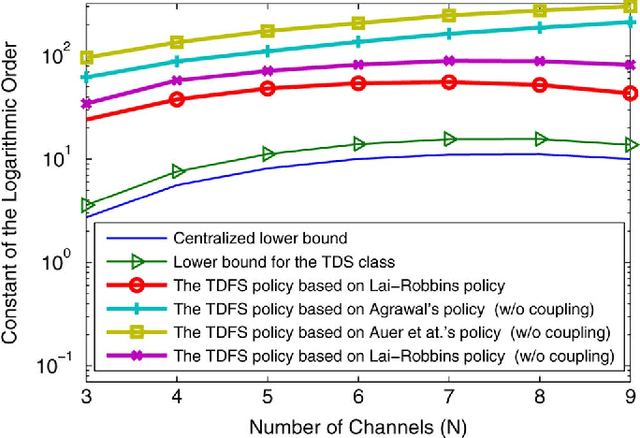
We formulate and study a decentralized multi-armed bandit (MAB) problem. There are M distributed players competing for N independent arms. Each arm, when played, offers i.i.d. reward according to a distribution with an unknown parameter. At each time, each player chooses one arm to play without exchanging observations or any information with other players. Players choosing the same arm collide, and, depending on the collision model, either no one receives reward or the colliding players share the reward in an arbitrary way. We show that the minimum system regret of the decentralized MAB grows with time at the same logarithmic order as in the centralized counterpart where players act collectively as a single entity by exchanging observations and making decisions jointly. A decentralized policy is constructed to achieve this optimal order while ensuring fairness among players and without assuming any pre-agreement or information exchange among players. Based on a Time Division Fair Sharing (TDFS) of the M best arms, the proposed policy is constructed and its order optimality is proven under a general reward model. Furthermore, the basic structure of the TDFS policy can be used with any order-optimal single-player policy to achieve order optimality in the decentralized setting. We also establish a lower bound on the system regret growth rate for a general class of decentralized polices, to which the proposed policy belongs. This problem finds potential applications in cognitive radio networks, multi-channel communication systems, multi-agent systems, web search and advertising, and social networks.