Temperature Balancing, Layer-wise Weight Analysis, and Neural Network Training

Regularization in modern machine learning is crucial, and it can take various forms in algorithmic design: training set, model family, error function, regularization terms, and optimizations. In particular, the learning rate, which can be interpreted as a temperature-like parameter within the statistical mechanics of learning, plays a crucial role in neural network training. Indeed, many widely adopted training strategies basically just define the decay of the learning rate over time. This process can be interpreted as decreasing a temperature, using either a global learning rate (for the entire model) or a learning rate that varies for each parameter. This paper proposes TempBalance, a straightforward yet effective layer-wise learning rate method. TempBalance is based on Heavy-Tailed Self-Regularization (HT-SR) Theory, an approach which characterizes the implicit self-regularization of different layers in trained models. We demonstrate the efficacy of using HT-SR-motivated metrics to guide the scheduling and balancing of temperature across all network layers during model training, resulting in improved performance during testing. We implement TempBalance on CIFAR10, CIFAR100, SVHN, and TinyImageNet datasets using ResNets, VGGs, and WideResNets with various depths and widths. Our results show that TempBalance significantly outperforms ordinary SGD and carefully-tuned spectral norm regularization. We also show that TempBalance outperforms a number of state-of-the-art optimizers and learning rate schedulers.

Evaluating natural language processing models with generalization metrics that do not need access to any training or testing data

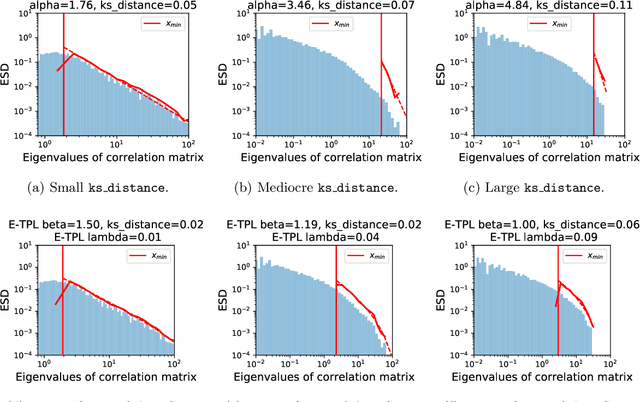
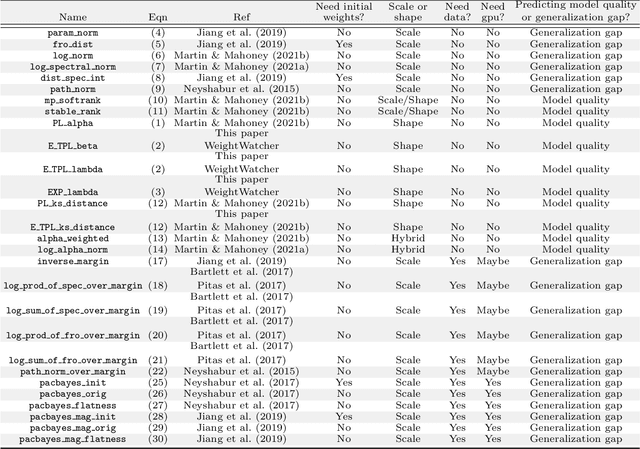
The search for effective and robust generalization metrics has been the focus of recent theoretical and empirical work. In this paper, we discuss the performance of natural language processing (NLP) models, and we evaluate various existing and novel generalization metrics. Compared to prior studies, we (i) focus on NLP instead of computer vision (CV), (ii) focus on generalization metrics that predict test error instead of the generalization gap, (iii) focus on generalization metrics that do not need the access to data, and (iv) focus on the heavy-tail (HT) phenomenon that has received comparatively less attention in the study of deep neural networks (NNs). We extend recent HT-based work which focuses on power law (PL) distributions, and we study exponential (EXP) and exponentially truncated power law (E-TPL) fitting to the empirical spectral densities (ESDs) of weight matrices. Our detailed empirical studies show that (i) \emph{shape metrics}, or the metrics obtained from fitting the shape of the ESDs, perform uniformly better at predicting generalization performance than \emph{scale metrics} commonly studied in the literature, as measured by the \emph{average} rank correlations with the generalization performance for all of our experiments; (ii) among forty generalization metrics studied in our paper, the \RANDDISTANCE metric, a new shape metric invented in this paper that measures the distance between empirical eigenvalues of weight matrices and those of randomly initialized weight matrices, achieves the highest worst-case rank correlation with generalization performance under a variety of training settings; and (iii) among the three HT distributions considered in our paper, the E-TPL fitting of ESDs performs the most robustly.

Post-mortem on a deep learning contest: a Simpson's paradox and the complementary roles of scale metrics versus shape metrics

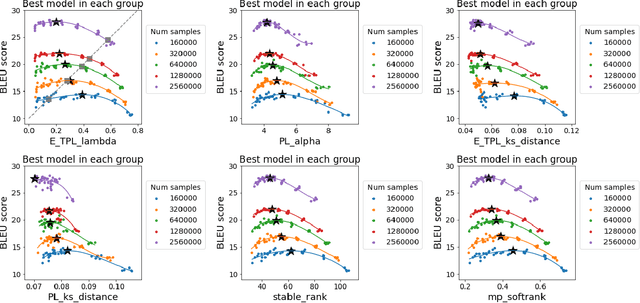
To understand better the causes of good generalization performance in state-of-the-art neural network (NN) models, we analyze of a corpus of models that was made publicly-available for a contest to predict the generalization accuracy of NNs. These models include a wide range of qualities and were trained with a range of architectures and regularization hyperparameters. We identify what amounts to a Simpson's paradox: where "scale" metrics (from traditional statistical learning theory) perform well overall but perform poorly on subpartitions of the data of a given depth, when regularization hyperparameters are varied; and where "shape" metrics (from Heavy-Tailed Self Regularization theory) perform well on subpartitions of the data, when hyperparameters are varied for models of a given depth, but perform poorly overall when models with varying depths are aggregated. Our results highlight the subtly of comparing models when both architectures and hyperparameters are varied, as well as the complementary role of implicit scale versus implicit shape parameters in understanding NN model quality. Our results also suggest caution when one tries to extract causal insight with a single metric applied to aggregate data, and they highlight the need to go beyond one-size-fits-all metrics based on upper bounds from generalization theory to describe the performance of state-of-the-art NN models. Based on these findings, we present two novel shape metrics, one data-independent, and the other data-dependent, which can predict trends in the test accuracy of a series of NNs, of a fixed architecture/depth, when varying solver hyperparameters.

Predicting trends in the quality of state-of-the-art neural networks without access to training or testing data

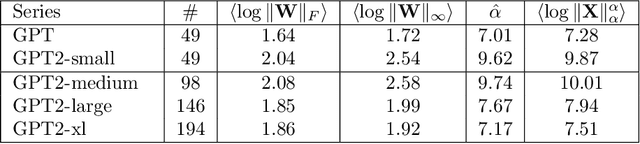
In many applications, one works with deep neural network (DNN) models trained by someone else. For such pretrained models, one typically does not have access to training/test data. Moreover, one does not know many details about the model, such as the specifics of the training data, the loss function, the hyperparameter values, etc. Given one or many pretrained models, can one say anything about the expected performance or quality of the models? Here, we present and evaluate empirical quality metrics for pretrained DNN models at scale. Using the open-source WeightWatcher tool, we analyze hundreds of publicly-available pretrained models, including older and current state-of-the-art models in CV and NLP. We examine norm-based capacity control metrics as well as newer Power Law (PL) based metrics (including fitted PL exponents and a Weighted Alpha metric), from the recently-developed Theory of Heavy-Tailed Self Regularization. Norm-based metrics correlate well with reported test accuracies for well-trained models across nearly all CV architecture series. On the other hand, norm-based metrics can not distinguish "good-versus-bad" models---which, arguably is the point of needing quality metrics. Indeed, they may give spurious results. PL-based metrics do much better---quantitatively better at discriminating series of "good-better-best" models, and qualitatively better at discriminating "good-versus-bad" models. PL-based metrics can also be used to characterize fine-scale properties of models, and we introduce the layer-wise Correlation Flow as new quality assessment. We show how poorly-trained (and/or poorly fine-tuned) models may exhibit both Scale Collapse and unusually large PL exponents, in particular for recent NLP models. Our techniques can be used to identify when a pretrained DNN has problems that can not be detected simply by examining training/test accuracies.

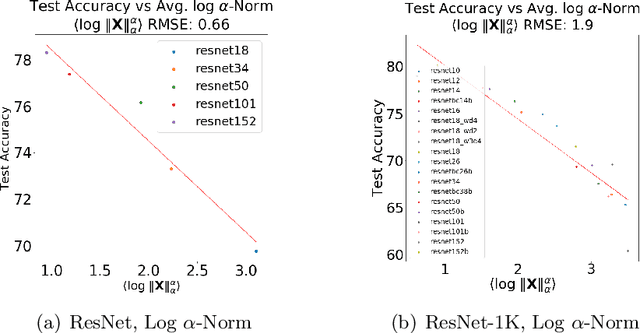
Heavy-Tailed Universality Predicts Trends in Test Accuracies for Very Large Pre-Trained Deep Neural Networks

Given two or more Deep Neural Networks (DNNs) with the same or similar architectures, and trained on the same dataset, but trained with different solvers, parameters, hyper-parameters, regularization, etc., can we predict which DNN will have the best test accuracy, and can we do so without peeking at the test data? In this paper, we show how to use a new Theory of Heavy-Tailed Self-Regularization (HT-SR) to answer this. HT-SR suggests, among other things, that modern DNNs exhibit what we call Heavy-Tailed Mechanistic Universality (HT-MU), meaning that the correlations in the layer weight matrices can be fit to a power law with exponents that lie in common Universality classes from Heavy-Tailed Random Matrix Theory (HT-RMT). From this, we develop a Universal capacity control metric that is a weighted average of these PL exponents. Rather than considering small toy NNs, we examine over 50 different, large-scale pre-trained DNNs, ranging over 15 different architectures, trained on ImagetNet, each of which has been reported to have different test accuracies. We show that this new capacity metric correlates very well with the reported test accuracies of these DNNs, looking across each architecture (VGG16/.../VGG19, ResNet10/.../ResNet152, etc.). We also show how to approximate the metric by the more familiar Product Norm capacity measure, as the average of the log Frobenius norm of the layer weight matrices. Our approach requires no changes to the underlying DNN or its loss function, it does not require us to train a model (although it could be used to monitor training), and it does not even require access to the ImageNet data.

Traditional and Heavy-Tailed Self Regularization in Neural Network Models

Random Matrix Theory (RMT) is applied to analyze the weight matrices of Deep Neural Networks (DNNs), including both production quality, pre-trained models such as AlexNet and Inception, and smaller models trained from scratch, such as LeNet5 and a miniature-AlexNet. Empirical and theoretical results clearly indicate that the empirical spectral density (ESD) of DNN layer matrices displays signatures of traditionally-regularized statistical models, even in the absence of exogenously specifying traditional forms of regularization, such as Dropout or Weight Norm constraints. Building on recent results in RMT, most notably its extension to Universality classes of Heavy-Tailed matrices, we develop a theory to identify \emph{5+1 Phases of Training}, corresponding to increasing amounts of \emph{Implicit Self-Regularization}. For smaller and/or older DNNs, this Implicit Self-Regularization is like traditional Tikhonov regularization, in that there is a `size scale' separating signal from noise. For state-of-the-art DNNs, however, we identify a novel form of \emph{Heavy-Tailed Self-Regularization}, similar to the self-organization seen in the statistical physics of disordered systems. This implicit Self-Regularization can depend strongly on the many knobs of the training process. By exploiting the generalization gap phenomena, we demonstrate that we can cause a small model to exhibit all 5+1 phases of training simply by changing the batch size.

Implicit Self-Regularization in Deep Neural Networks: Evidence from Random Matrix Theory and Implications for Learning

Random Matrix Theory (RMT) is applied to analyze weight matrices of Deep Neural Networks (DNNs), including both production quality, pre-trained models such as AlexNet and Inception, and smaller models trained from scratch, such as LeNet5 and a miniature-AlexNet. Empirical and theoretical results clearly indicate that the DNN training process itself implicitly implements a form of Self-Regularization. The empirical spectral density (ESD) of DNN layer matrices displays signatures of traditionally-regularized statistical models, even in the absence of exogenously specifying traditional forms of explicit regularization. Building on relatively recent results in RMT, most notably its extension to Universality classes of Heavy-Tailed matrices, we develop a theory to identify 5+1 Phases of Training, corresponding to increasing amounts of Implicit Self-Regularization. These phases can be observed during the training process as well as in the final learned DNNs. For smaller and/or older DNNs, this Implicit Self-Regularization is like traditional Tikhonov regularization, in that there is a "size scale" separating signal from noise. For state-of-the-art DNNs, however, we identify a novel form of Heavy-Tailed Self-Regularization, similar to the self-organization seen in the statistical physics of disordered systems. This results from correlations arising at all size scales, which arises implicitly due to the training process itself. This implicit Self-Regularization can depend strongly on the many knobs of the training process. By exploiting the generalization gap phenomena, we demonstrate that we can cause a small model to exhibit all 5+1 phases of training simply by changing the batch size. This demonstrates that---all else being equal---DNN optimization with larger batch sizes leads to less-well implicitly-regularized models, and it provides an explanation for the generalization gap phenomena.

Rethinking generalization requires revisiting old ideas: statistical mechanics approaches and complex learning behavior

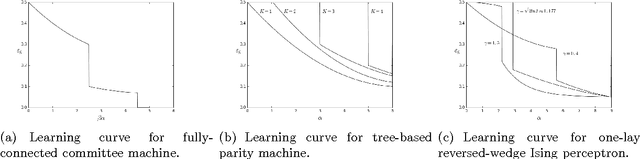
We describe an approach to understand the peculiar and counterintuitive generalization properties of deep neural networks. The approach involves going beyond worst-case theoretical capacity control frameworks that have been popular in machine learning in recent years to revisit old ideas in the statistical mechanics of neural networks. Within this approach, we present a prototypical Very Simple Deep Learning (VSDL) model, whose behavior is controlled by two control parameters, one describing an effective amount of data, or load, on the network (that decreases when noise is added to the input), and one with an effective temperature interpretation (that increases when algorithms are early stopped). Using this model, we describe how a very simple application of ideas from the statistical mechanics theory of generalization provides a strong qualitative description of recently-observed empirical results regarding the inability of deep neural networks not to overfit training data, discontinuous learning and sharp transitions in the generalization properties of learning algorithms, etc.