Whittle Index for A Class of Restless Bandits with Imperfect Observations

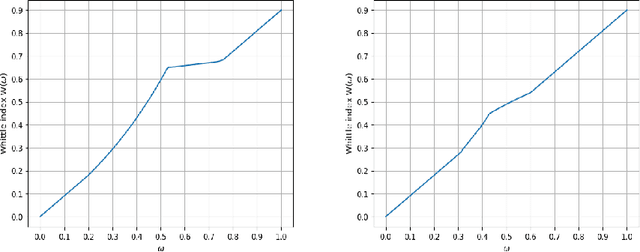
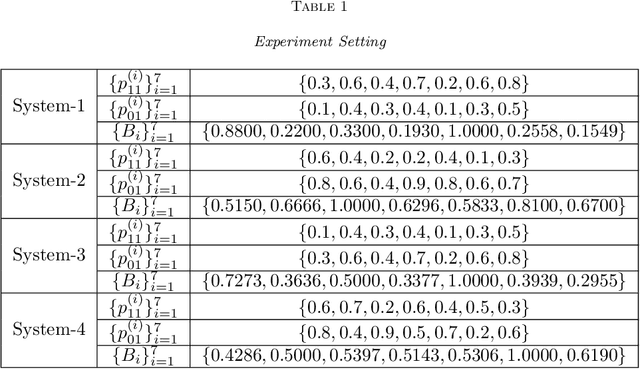
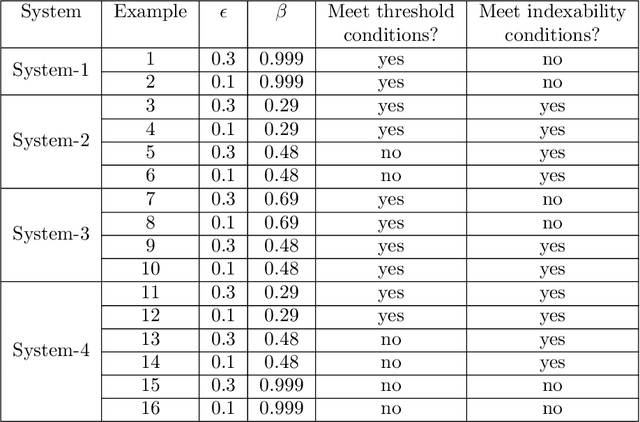
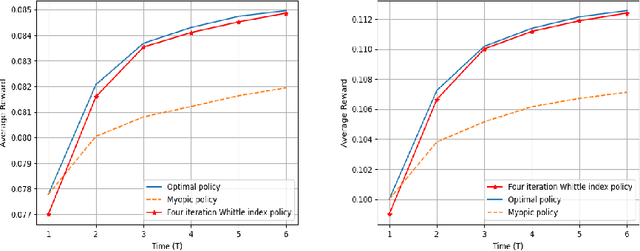
We consider a class of restless bandit problems that finds a broad application area in stochastic optimization, reinforcement learning and operations research. In our model, there are $N$ independent $2$-state Markov processes that may be observed and accessed for accruing rewards. The observation is error-prone, i.e., both false alarm and miss detection may happen. Furthermore, the user can only choose a subset of $M~(M<N)$ processes to observe at each discrete time. If a process in state~$1$ is correctly observed, then it will offer some reward. Due to the partial and imperfect observation model, the system is formulated as a restless multi-armed bandit problem with an information state space of uncountable cardinality. Restless bandit problems with finite state spaces are PSPACE-HARD in general. In this paper, we establish a low-complexity algorithm that achieves a strong performance for this class of restless bandits. Under certain conditions, we theoretically prove the existence (indexability) of Whittle index and its equivalence to our algorithm. When those conditions do not hold, we show by numerical experiments the near-optimal performance of our algorithm in general.