Distributed Learning in Multi-Armed Bandit with Multiple Players
Paper and Code
Jun 07, 2010


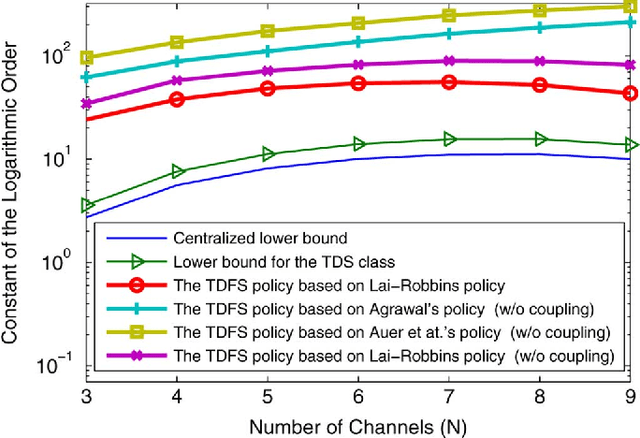
We formulate and study a decentralized multi-armed bandit (MAB) problem. There are M distributed players competing for N independent arms. Each arm, when played, offers i.i.d. reward according to a distribution with an unknown parameter. At each time, each player chooses one arm to play without exchanging observations or any information with other players. Players choosing the same arm collide, and, depending on the collision model, either no one receives reward or the colliding players share the reward in an arbitrary way. We show that the minimum system regret of the decentralized MAB grows with time at the same logarithmic order as in the centralized counterpart where players act collectively as a single entity by exchanging observations and making decisions jointly. A decentralized policy is constructed to achieve this optimal order while ensuring fairness among players and without assuming any pre-agreement or information exchange among players. Based on a Time Division Fair Sharing (TDFS) of the M best arms, the proposed policy is constructed and its order optimality is proven under a general reward model. Furthermore, the basic structure of the TDFS policy can be used with any order-optimal single-player policy to achieve order optimality in the decentralized setting. We also establish a lower bound on the system regret growth rate for a general class of decentralized polices, to which the proposed policy belongs. This problem finds potential applications in cognitive radio networks, multi-channel communication systems, multi-agent systems, web search and advertising, and social networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge