Deterministic Sequencing of Exploration and Exploitation for Multi-Armed Bandit Problems

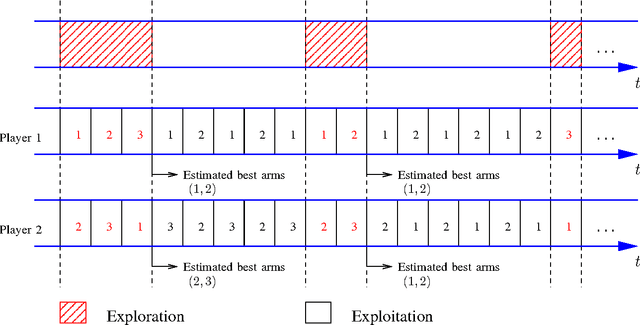
In the Multi-Armed Bandit (MAB) problem, there is a given set of arms with unknown reward models. At each time, a player selects one arm to play, aiming to maximize the total expected reward over a horizon of length T. An approach based on a Deterministic Sequencing of Exploration and Exploitation (DSEE) is developed for constructing sequential arm selection policies. It is shown that for all light-tailed reward distributions, DSEE achieves the optimal logarithmic order of the regret, where regret is defined as the total expected reward loss against the ideal case with known reward models. For heavy-tailed reward distributions, DSEE achieves O(T^1/p) regret when the moments of the reward distributions exist up to the pth order for 1<p<=2 and O(T^1/(1+p/2)) for p>2. With the knowledge of an upperbound on a finite moment of the heavy-tailed reward distributions, DSEE offers the optimal logarithmic regret order. The proposed DSEE approach complements existing work on MAB by providing corresponding results for general reward distributions. Furthermore, with a clearly defined tunable parameter-the cardinality of the exploration sequence, the DSEE approach is easily extendable to variations of MAB, including MAB with various objectives, decentralized MAB with multiple players and incomplete reward observations under collisions, MAB with unknown Markov dynamics, and combinatorial MAB with dependent arms that often arise in network optimization problems such as the shortest path, the minimum spanning, and the dominating set problems under unknown random weights.