ACIL: Analytic Class-Incremental Learning with Absolute Memorization and Privacy Protection

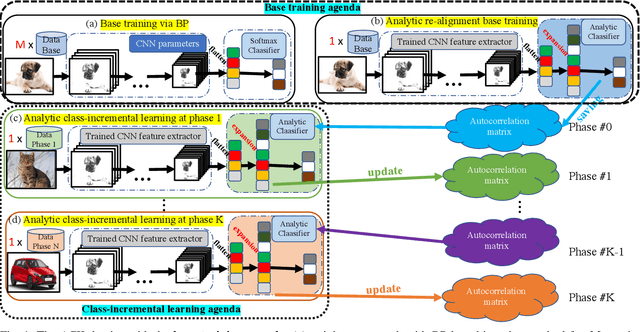
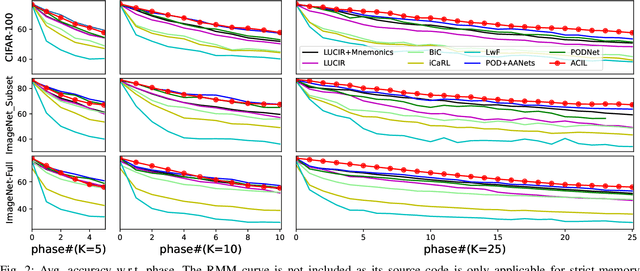
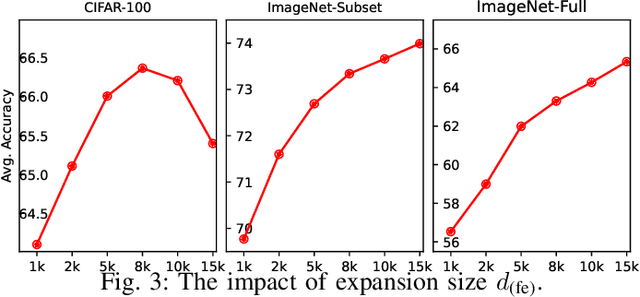
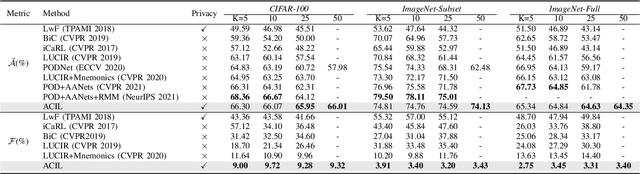
Class-incremental learning (CIL) learns a classification model with training data of different classes arising progressively. Existing CIL either suffers from serious accuracy loss due to catastrophic forgetting, or invades data privacy by revisiting used exemplars. Inspired by linear learning formulations, we propose an analytic class-incremental learning (ACIL) with absolute memorization of past knowledge while avoiding breaching of data privacy (i.e., without storing historical data). The absolute memorization is demonstrated in the sense that class-incremental learning using ACIL given present data would give identical results to that from its joint-learning counterpart which consumes both present and historical samples. This equality is theoretically validated. Data privacy is ensured since no historical data are involved during the learning process. Empirical validations demonstrate ACIL's competitive accuracy performance with near-identical results for various incremental task settings (e.g., 5-50 phases). This also allows ACIL to outperform the state-of-the-art methods for large-phase scenarios (e.g., 25 and 50 phases).

Deterministic Bridge Regression for Compressive Classification

Pattern classification with compact representation is an important component in machine intelligence. In this work, an analytic bridge solution is proposed for compressive classification. The proposal has been based upon solving a penalized error formulation utilizing an approximated $\ell_p$-norm. The solution comes in a primal form for over-determined systems and in a dual form for under-determined systems. While the primal form is suitable for problems of low dimension with large data samples, the dual form is suitable for problems of high dimension but with a small number of data samples. The solution has also been extended for problems with multiple classification outputs. Numerical studies based on simulated and real-world data validated the effectiveness of the proposed solution.

Analytic Learning of Convolutional Neural Network For Pattern Recognition

Training convolutional neural networks (CNNs) with back-propagation (BP) is time-consuming and resource-intensive particularly in view of the need to visit the dataset multiple times. In contrast, analytic learning attempts to obtain the weights in one epoch. However, existing attempts to analytic learning considered only the multilayer perceptron (MLP). In this article, we propose an analytic convolutional neural network learning (ACnnL). Theoretically we show that ACnnL builds a closed-form solution similar to its MLP counterpart, but differs in their regularization constraints. Consequently, we are able to answer to a certain extent why CNNs usually generalize better than MLPs from the implicit regularization point of view. The ACnnL is validated by conducting classification tasks on several benchmark datasets. It is encouraging that the ACnnL trains CNNs in a significantly fast manner with reasonably close prediction accuracies to those using BP. Moreover, our experiments disclose a unique advantage of ACnnL under the small-sample scenario when training data are scarce or expensive.

An Analytic Layer-wise Deep Learning Framework with Applications to Robotics

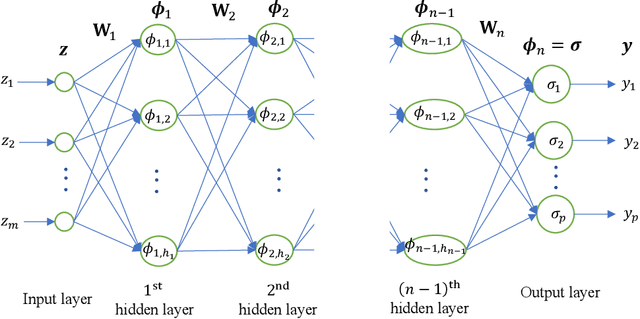
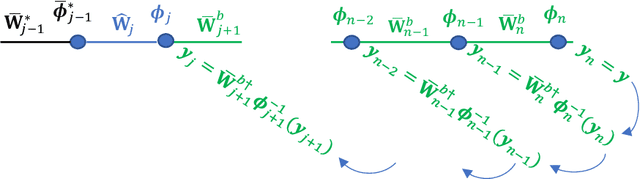
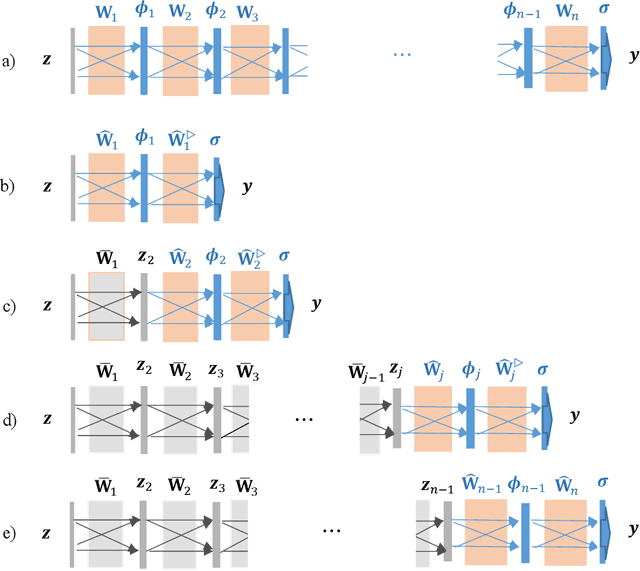
Deep learning has achieved great success in many applications, but it has been less well analyzed from the theoretical perspective. To deploy deep learning algorithms in a predictable and stable manner is particularly important in robotics, as robots are active agents that need to interact safely with the physical world. This paper presents an analytic deep learning framework for fully connected neural networks, which can be applied for both regression problems and classification problems. Examples for regression and classification problems include online robot control and robot vision. We present two layer-wise learning algorithms such that the convergence of the learning systems can be analyzed. Firstly, an inverse layer-wise learning algorithm for multilayer networks with convergence analysis for each layer is presented to understand the problems of layer-wise deep learning. Secondly, a forward progressive learning algorithm where the deep networks are built progressively by using single hidden layer networks is developed to achieve better accuracy. It is shown that the progressive learning method can be used for fine-tuning of weights from convergence point of view. The effectiveness of the proposed framework is illustrated based on classical benchmark recognition tasks using the MNIST and CIFAR-10 datasets and the results show a good balance between performance and explainability. The proposed method is subsequently applied for online learning of robot kinematics and experimental results on kinematic control of UR5e robot with unknown model are presented.

Accumulated Decoupled Learning: Mitigating Gradient Staleness in Inter-Layer Model Parallelization

Decoupled learning is a branch of model parallelism which parallelizes the training of a network by splitting it depth-wise into multiple modules. Techniques from decoupled learning usually lead to stale gradient effect because of their asynchronous implementation, thereby causing performance degradation. In this paper, we propose an accumulated decoupled learning (ADL) which incorporates the gradient accumulation technique to mitigate the stale gradient effect. We give both theoretical and empirical evidences regarding how the gradient staleness can be reduced. We prove that the proposed method can converge to critical points, i.e., the gradients converge to 0, in spite of its asynchronous nature. Empirical validation is provided by training deep convolutional neural networks to perform classification tasks on CIFAR-10 and ImageNet datasets. The ADL is shown to outperform several state-of-the-arts in the classification tasks, and is the fastest among the compared methods.

Analytic Network Learning

Based on the property that solving the system of linear matrix equations via the column space and the row space projections boils down to an approximation in the least squares error sense, a formulation for learning the weight matrices of the multilayer network can be derived. By exploiting into the vast number of feasible solutions of these interdependent weight matrices, the learning can be performed analytically layer by layer without needing of gradient computation after an initialization. Possible initialization schemes include utilizing the data matrix as initial weights and random initialization. The study is followed by an investigation into the representation capability and the output variance of the learning scheme. An extensive experimentation on synthetic and real-world data sets validates its numerical feasibility.

Gradient-Free Learning Based on the Kernel and the Range Space

In this article, we show that solving the system of linear equations by manipulating the kernel and the range space is equivalent to solving the problem of least squares error approximation. This establishes the ground for a gradient-free learning search when the system can be expressed in the form of a linear matrix equation. When the nonlinear activation function is invertible, the learning problem of a fully-connected multilayer feedforward neural network can be easily adapted for this novel learning framework. By a series of kernel and range space manipulations, it turns out that such a network learning boils down to solving a set of cross-coupling equations. By having the weights randomly initialized, the equations can be decoupled and the network solution shows relatively good learning capability for real world data sets of small to moderate dimensions. Based on the structural information of the matrix equation, the network representation is found to be dependent on the number of data samples and the output dimension.

Learning from the Kernel and the Range Space

In this article, a novel approach to learning a complex function which can be written as the system of linear equations is introduced. This learning is grounded upon the observation that solving the system of linear equations by a manipulation in the kernel and the range space boils down to an estimation based on the least squares error approximation. The learning approach is applied to learn a deep feedforward network with full weight connections. The numerical experiments on network learning of synthetic and benchmark data not only show feasibility of the proposed learning approach but also provide insights into the mechanism of data representation.

Deterministic Stretchy Regression

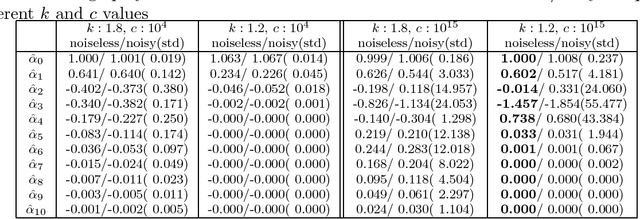
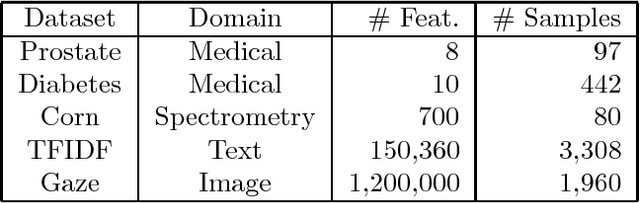
An extension of the regularized least-squares in which the estimation parameters are stretchable is introduced and studied in this paper. The solution of this ridge regression with stretchable parameters is given in primal and dual spaces and in closed-form. Essentially, the proposed solution stretches the covariance computation by a power term, thereby compressing or amplifying the estimation parameters. To maintain the computation of power root terms within the real space, an input transformation is proposed. The results of an empirical evaluation in both synthetic and real-world data illustrate that the proposed method is effective for compressive learning with high-dimensional data.

Stretchy Polynomial Regression

This article proposes a novel solution for stretchy polynomial regression learning. The solution comes in primal and dual closed-forms similar to that of ridge regression. Essentially, the proposed solution stretches the covariance computation via a power term thereby compresses or amplifies the estimation. Our experiments on both synthetic data and real-world data show effectiveness of the proposed method for compressive learning.