Deterministic Stretchy Regression
Paper and Code
Jun 09, 2018
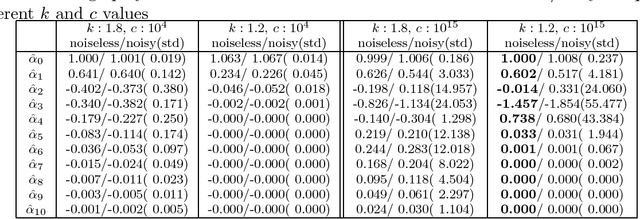

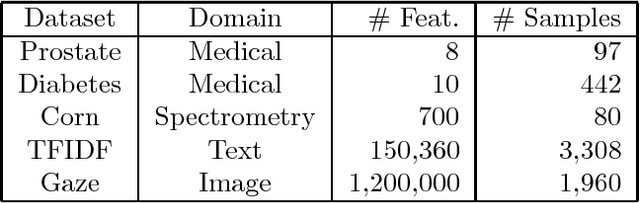
An extension of the regularized least-squares in which the estimation parameters are stretchable is introduced and studied in this paper. The solution of this ridge regression with stretchable parameters is given in primal and dual spaces and in closed-form. Essentially, the proposed solution stretches the covariance computation by a power term, thereby compressing or amplifying the estimation parameters. To maintain the computation of power root terms within the real space, an input transformation is proposed. The results of an empirical evaluation in both synthetic and real-world data illustrate that the proposed method is effective for compressive learning with high-dimensional data.
* Submitted for journal (JMLR) review since 28-Sept-2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge