Sequence-of-Constraints MPC: Reactive Timing-Optimal Control of Sequential Manipulation

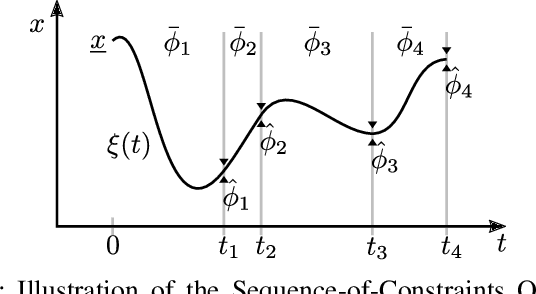
Task and Motion Planning has made great progress in solving hard sequential manipulation problems. However, a gap between such planning formulations and control methods for reactive execution remains. In this paper we propose a model predictive control approach dedicated to robustly execute a single sequence of constraints, which corresponds to a discrete decision sequence of a TAMP plan. We decompose the overall control problem into three sub-problems (solving for sequential waypoints, their timing, and a short receding horizon path) that each is a non-linear program solved online in each MPC cycle. The resulting control strategy can account for long-term interdependencies of constraints and reactively plan for a timing-optimal transition through all constraints. We additionally propose phase backtracking when running constraints are missed, leading to a fluent re-initiation behavior that is robust to perturbations and interferences by an experimenter.

Learning Neural Implicit Functions as Object Representations for Robotic Manipulation

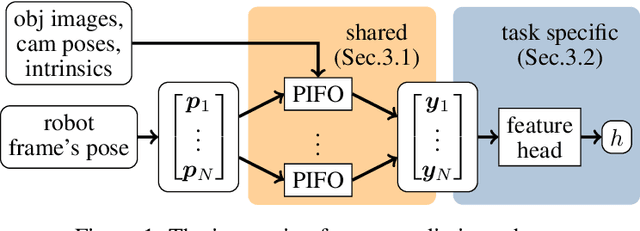
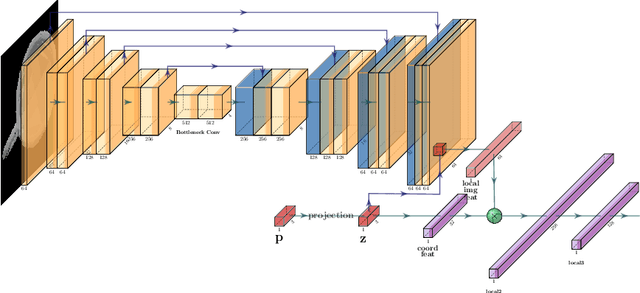
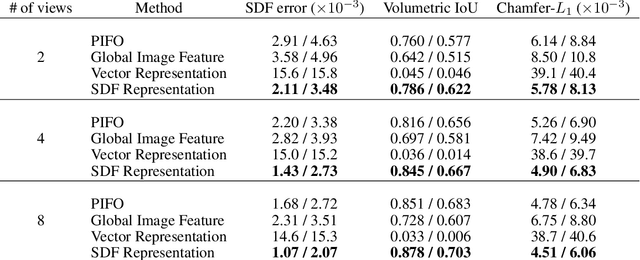
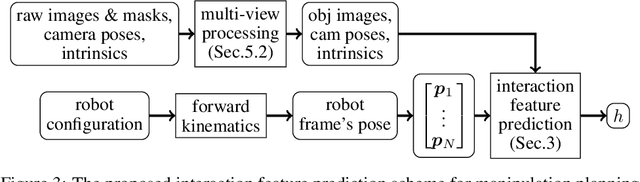
Robotic manipulation planning is the problem of finding a sequence of robot configurations that involves interactions with objects in the scene, e.g., grasp, placement, tool-use, etc. To achieve such interactions, traditional approaches require hand-designed features and object representations, and it still remains an open question how to describe such interactions with arbitrary objects in a flexible and efficient way. Inspired by recent advances in 3D modeling, e.g. NeRF, we propose a method to represent objects as neural implicit functions upon which we can define and jointly train interaction constraint functions. The proposed pixel-aligned representation is directly inferred from camera images with known camera geometry, naturally acting as a perception component in the whole manipulation pipeline, while at the same time enabling sequential robot manipulation planning.

Learning Models as Functionals of Signed-Distance Fields for Manipulation Planning

This work proposes an optimization-based manipulation planning framework where the objectives are learned functionals of signed-distance fields that represent objects in the scene. Most manipulation planning approaches rely on analytical models and carefully chosen abstractions/state-spaces to be effective. A central question is how models can be obtained from data that are not primarily accurate in their predictions, but, more importantly, enable efficient reasoning within a planning framework, while at the same time being closely coupled to perception spaces. We show that representing objects as signed-distance fields not only enables to learn and represent a variety of models with higher accuracy compared to point-cloud and occupancy measure representations, but also that SDF-based models are suitable for optimization-based planning. To demonstrate the versatility of our approach, we learn both kinematic and dynamic models to solve tasks that involve hanging mugs on hooks and pushing objects on a table. We can unify these quite different tasks within one framework, since SDFs are the common object representation. Video: https://youtu.be/ga8Wlkss7co

Distilling a Hierarchical Policy for Planning and Control via Representation and Reinforcement Learning

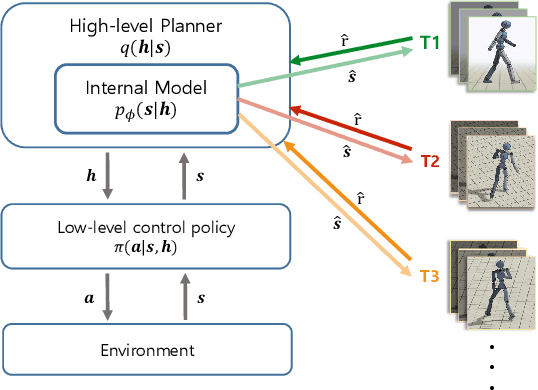
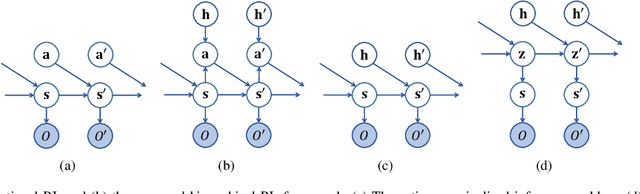
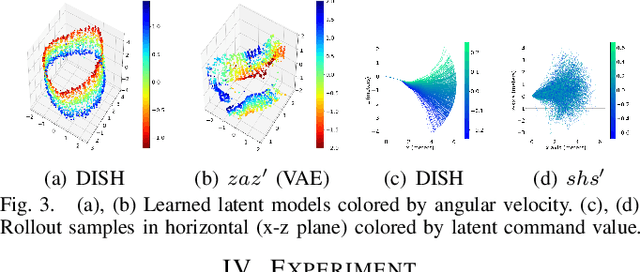
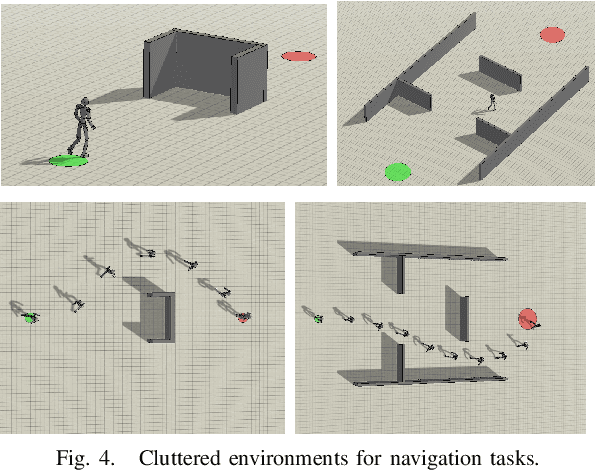
We present a hierarchical planning and control framework that enables an agent to perform various tasks and adapt to a new task flexibly. Rather than learning an individual policy for each particular task, the proposed framework, DISH, distills a hierarchical policy from a set of tasks by representation and reinforcement learning. The framework is based on the idea of latent variable models that represent high-dimensional observations using low-dimensional latent variables. The resulting policy consists of two levels of hierarchy: (i) a planning module that reasons a sequence of latent intentions that would lead to an optimistic future and (ii) a feedback control policy, shared across the tasks, that executes the inferred intention. Because the planning is performed in low-dimensional latent space, the learned policy can immediately be used to solve or adapt to new tasks without additional training. We demonstrate the proposed framework can learn compact representations (3- and 1-dimensional latent states and commands for a humanoid with 197- and 36-dimensional state features and actions) while solving a small number of imitation tasks, and the resulting policy is directly applicable to other types of tasks, i.e., navigation in cluttered environments.

Deep Visual Reasoning: Learning to Predict Action Sequences for Task and Motion Planning from an Initial Scene Image

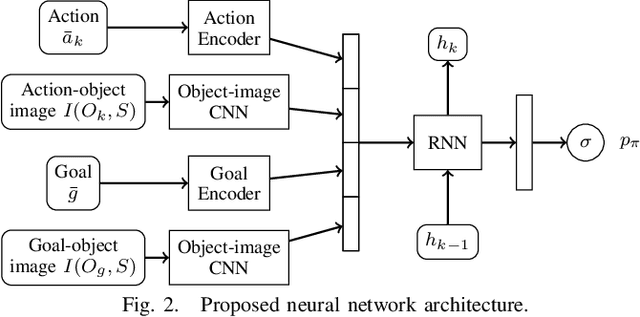
In this paper, we propose a deep convolutional recurrent neural network that predicts action sequences for task and motion planning (TAMP) from an initial scene image. Typical TAMP problems are formalized by combining reasoning on a symbolic, discrete level (e.g. first-order logic) with continuous motion planning such as nonlinear trajectory optimization. Due to the great combinatorial complexity of possible discrete action sequences, a large number of optimization/motion planning problems have to be solved to find a solution, which limits the scalability of these approaches. To circumvent this combinatorial complexity, we develop a neural network which, based on an initial image of the scene, directly predicts promising discrete action sequences such that ideally only one motion planning problem has to be solved to find a solution to the overall TAMP problem. A key aspect is that our method generalizes to scenes with many and varying number of objects, although being trained on only two objects at a time. This is possible by encoding the objects of the scene in images as input to the neural network, instead of a fixed feature vector. Results show runtime improvements of several magnitudes. Video: https://youtu.be/i8yyEbbvoEk

Probabilistic Framework for Constrained Manipulations and Task and Motion Planning under Uncertainty

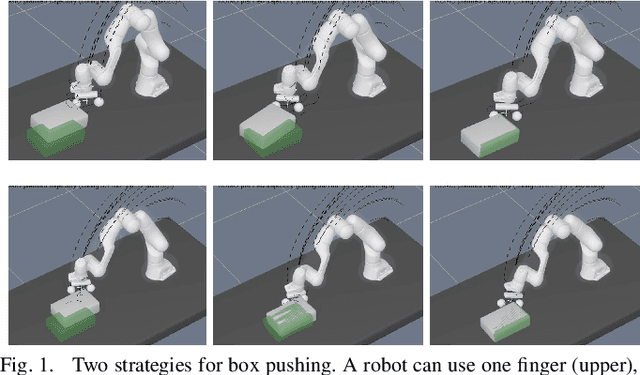
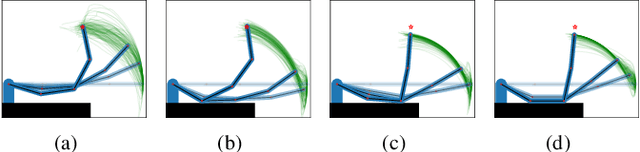
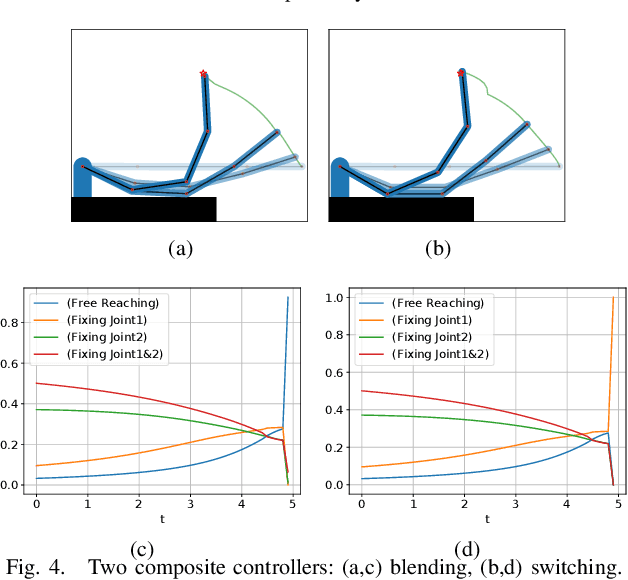
Logic-Geometric Programming (LGP) is a powerful motion and manipulation planning framework, which represents hierarchical structure using logic rules that describe discrete aspects of problems, e.g., touch, grasp, hit, or push, and solves the resulting smooth trajectory optimization. The expressive power of logic allows LGP for handling complex, large-scale sequential manipulation and tool-use planning problems. In this paper, we extend the LGP formulation to stochastic domains. Based on the control-inference duality, we interpret LGP in a stochastic domain as fitting a mixture of Gaussians to the posterior path distribution, where each logic profile defines a single Gaussian path distribution. The proposed framework enables a robot to prioritize various interaction modes and to acquire interesting behaviors such as contact exploitation for uncertainty reduction, eventually providing a composite control scheme that is reactive to disturbance. The supplementary video can be found at https://youtu.be/CEaJdVlSZyo

Describing Physics For Physical Reasoning: Force-based Sequential Manipulation Planning

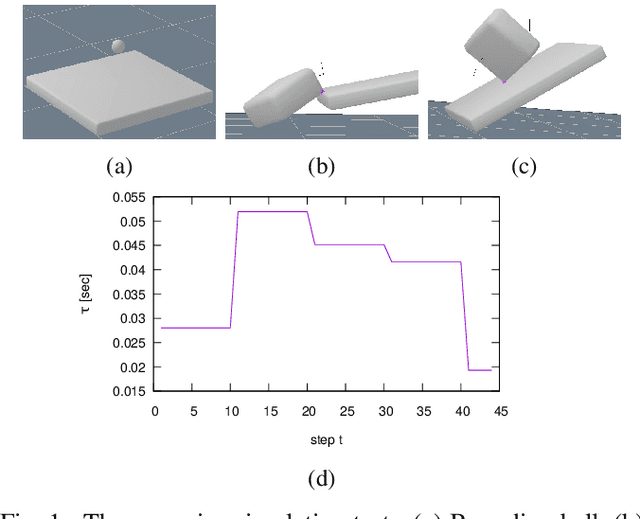
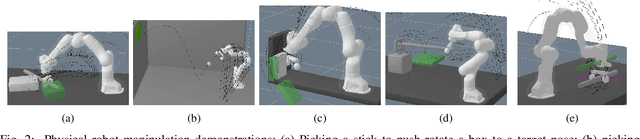
Physical reasoning is a core aspect of intelligence in animals and humans. A central question is what model should be used as a basis for reasoning. Existing work considered models ranging from intuitive physics and physical simulators to contact dynamics models used in robotic manipulation and locomotion. In this work we propose path descriptions of physics which directly allow us to leverage optimization methods to solve planning problems, using multi-physics descriptions that enable the solver to mix various levels of abstraction and simplifications for different objects and phases of the solution. We demonstrate the approach on various robot manipulation planning problems, such as grasping a stick in order to push or lift another object to a target, shifting and grasping a book from a shelve, and throwing an object to bounce towards a target.

A Distributed ADMM Approach to Informative Trajectory Planning for Multi-Target Tracking

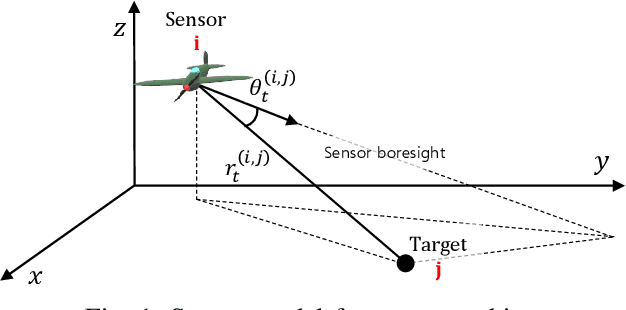
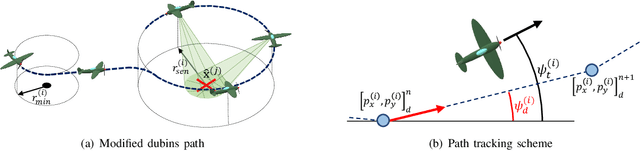
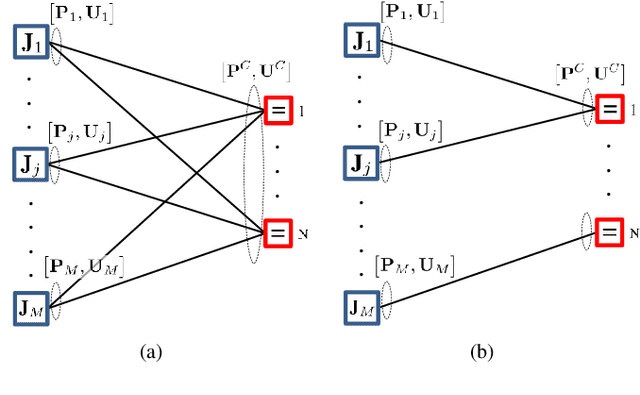
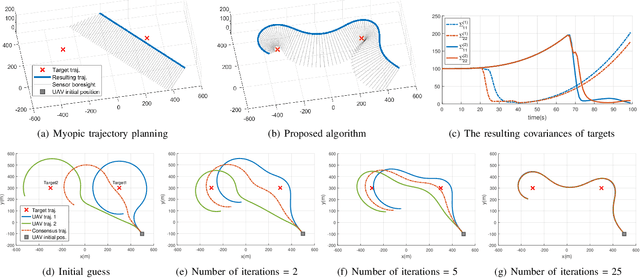
This paper presents a distributed optimization method for informative trajectory planning in multi-target tracking problems. The purpose of such problems is to optimize a sequence of waypoints/control inputs of mobile sensors over a certain future time step to minimize the uncertainty of targets. The planning problem is reformulated as a distributed optimization problem that can be expressed in the form of a subproblem for each target. The subproblems are coupled using the distributed Alternating Direction Method of Multipliers (ADMM). This coupling not only enables the results of each subproblem to be reflected in the optimization process of the other subproblems, but also guides the results of the subproblems to converge to the same solution. In contrast to the existing approaches performing trajectory optimization after assigning tasks, the proposed algorithm does not require the design of a heuristic cost function for task assignment, and it can handle both trajectory optimization and task assignment in multiple target tracking problems simultaneously. In order to reduce the computation time of the algorithm, an edge-cutting method suitable for multiple-target tracking problems is proposed, as is a receding horizon control scheme for real-time implementation, which considers the computation time. Numerical examples are presented to demonstrate the applicability of the algorithm.

Adaptive Path-Integral Autoencoder: Representation Learning and Planning for Dynamical Systems

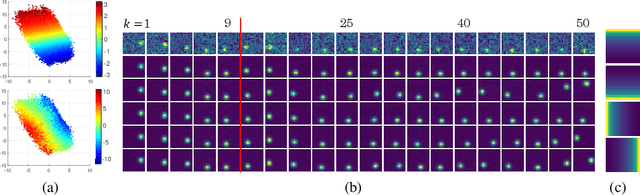
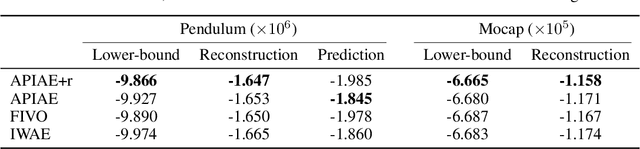
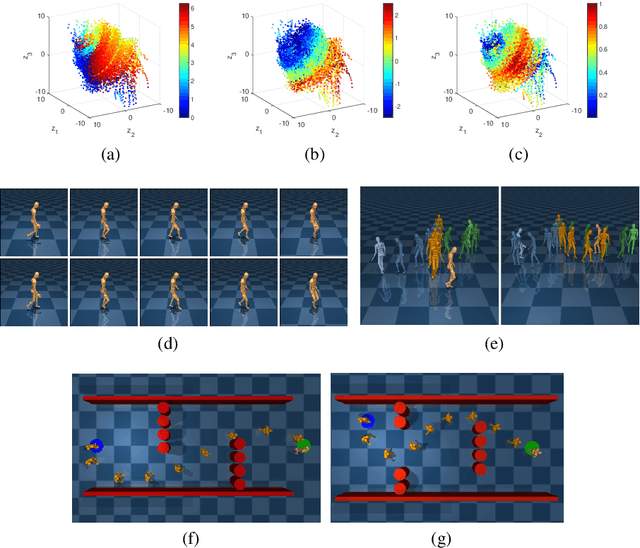
We present a representation learning algorithm that learns a low-dimensional latent dynamical system from high-dimensional \textit{sequential} raw data, e.g., video. The framework builds upon recent advances in amortized inference methods that use both an inference network and a refinement procedure to output samples from a variational distribution given an observation sequence, and takes advantage of the duality between control and inference to approximately solve the intractable inference problem using the path integral control approach. The learned dynamical model can be used to predict and plan the future states; we also present the efficient planning method that exploits the learned low-dimensional latent dynamics. Numerical experiments show that the proposed path-integral control based variational inference method leads to tighter lower bounds in statistical model learning of sequential data. The supplementary video: https://youtu.be/xCp35crUoLQ

Topology-Guided Path Integral Approach for Stochastic Optimal Control in Cluttered Environment

This paper addresses planning and control of robot motion under uncertainty that is formulated as a continuous-time, continuous-space stochastic optimal control problem, by developing a topology-guided path integral control method. The path integral control framework, which forms the backbone of the proposed method, re-writes the Hamilton-Jacobi-Bellman equation as a statistical inference problem; the resulting inference problem is solved by a sampling procedure that computes the distribution of controlled trajectories around the trajectory by the passive dynamics. For motion control of robots in a highly cluttered environment, however, this sampling can easily be trapped in a local minimum unless the sample size is very large, since the global optimality of local minima depends on the degree of uncertainty. Thus, a homology-embedded sampling-based planner that identifies many (potentially) local-minimum trajectories in different homology classes is developed to aid the sampling process. In combination with a receding-horizon fashion of the optimal control the proposed method produces a dynamically feasible and collision-free motion plans without being trapped in a local minimum. Numerical examples on a synthetic toy problem and on quadrotor control in a complex obstacle field demonstrate the validity of the proposed method.