Distilling a Hierarchical Policy for Planning and Control via Representation and Reinforcement Learning

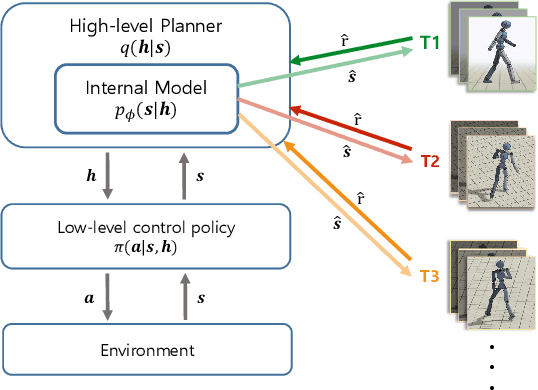
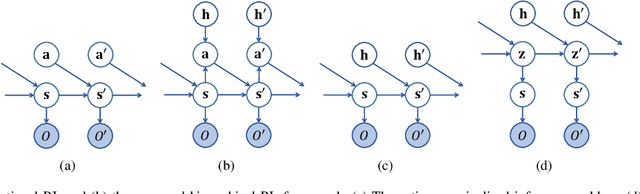
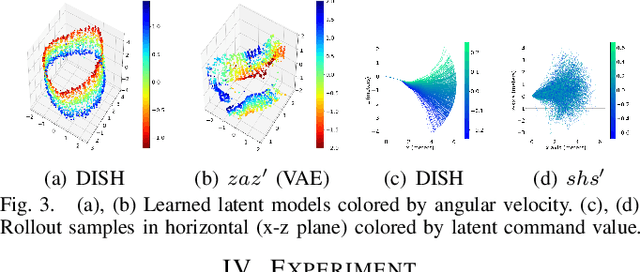
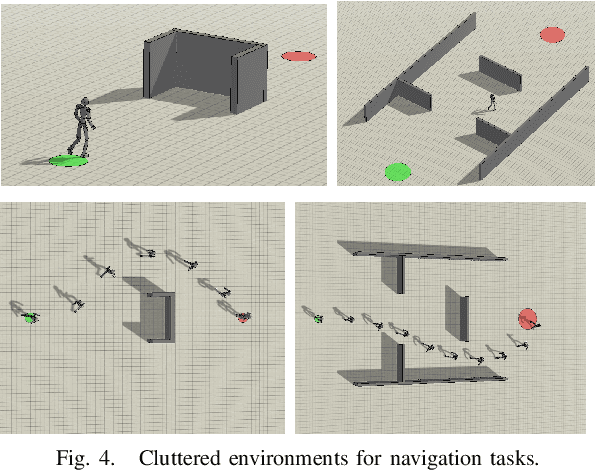
We present a hierarchical planning and control framework that enables an agent to perform various tasks and adapt to a new task flexibly. Rather than learning an individual policy for each particular task, the proposed framework, DISH, distills a hierarchical policy from a set of tasks by representation and reinforcement learning. The framework is based on the idea of latent variable models that represent high-dimensional observations using low-dimensional latent variables. The resulting policy consists of two levels of hierarchy: (i) a planning module that reasons a sequence of latent intentions that would lead to an optimistic future and (ii) a feedback control policy, shared across the tasks, that executes the inferred intention. Because the planning is performed in low-dimensional latent space, the learned policy can immediately be used to solve or adapt to new tasks without additional training. We demonstrate the proposed framework can learn compact representations (3- and 1-dimensional latent states and commands for a humanoid with 197- and 36-dimensional state features and actions) while solving a small number of imitation tasks, and the resulting policy is directly applicable to other types of tasks, i.e., navigation in cluttered environments.

Online Gaussian Process State-Space Models: Learning and Planning for Partially Observable Dynamical Systems

Gaussian process state-space model (GPSSM) is a probabilistic dynamical system that represents unknown transition and/or measurement models as the Gaussian process (GP). The majority of approaches to learning GPSSM are focused on handling given time series data. However, in most dynamical systems, data required for model learning arrives sequentially and accumulates over time. Storing all the data requires large ammounts of memory, and using it for model learning can be computationally infeasible. To overcome this challenge, this paper develops an online inference method for learning the GPSSM (onlineGPSSM) that fuses stochastic variational inference (VI) and online VI. The proposed method can mitigate the computation time issue without catastrophic forgetting and supports adaptation to changes in a system and/or a real environments. Furthermore, we propose a GPSSM-based reinforcement learning (RL) framework for partially observable dynamical systems by combining onlineGPSSM with Bayesian filtering and trajectory optimization algorithms. Numerical examples are presented to demonstrate the applicability of the proposed method.

A Distributed ADMM Approach to Informative Trajectory Planning for Multi-Target Tracking

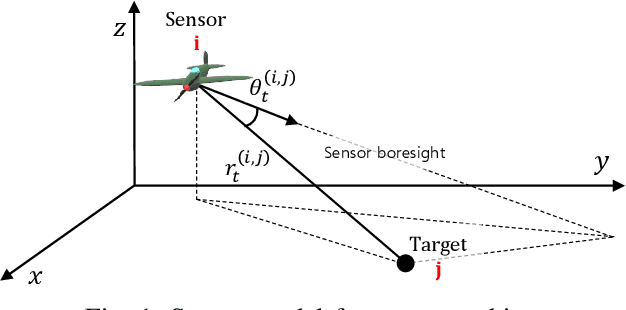
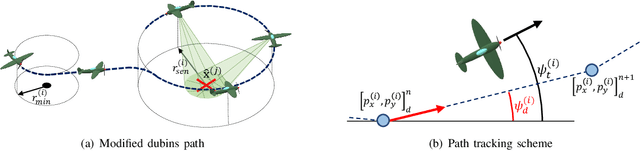
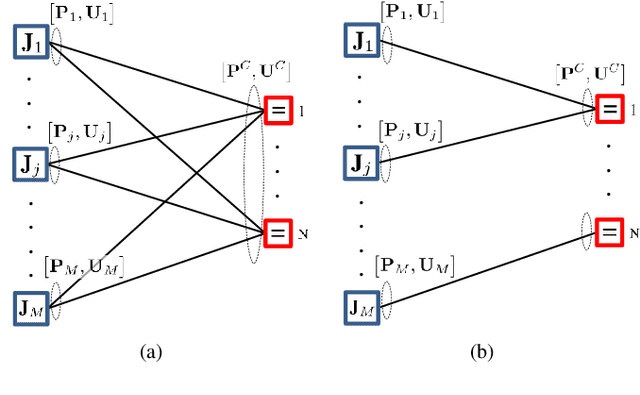
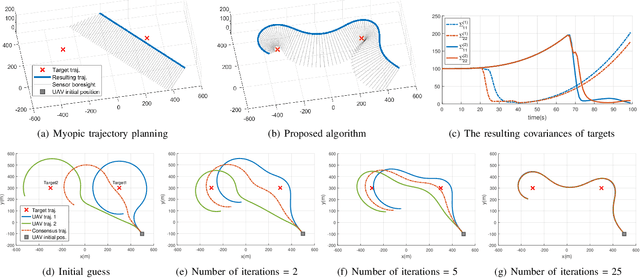
This paper presents a distributed optimization method for informative trajectory planning in multi-target tracking problems. The purpose of such problems is to optimize a sequence of waypoints/control inputs of mobile sensors over a certain future time step to minimize the uncertainty of targets. The planning problem is reformulated as a distributed optimization problem that can be expressed in the form of a subproblem for each target. The subproblems are coupled using the distributed Alternating Direction Method of Multipliers (ADMM). This coupling not only enables the results of each subproblem to be reflected in the optimization process of the other subproblems, but also guides the results of the subproblems to converge to the same solution. In contrast to the existing approaches performing trajectory optimization after assigning tasks, the proposed algorithm does not require the design of a heuristic cost function for task assignment, and it can handle both trajectory optimization and task assignment in multiple target tracking problems simultaneously. In order to reduce the computation time of the algorithm, an edge-cutting method suitable for multiple-target tracking problems is proposed, as is a receding horizon control scheme for real-time implementation, which considers the computation time. Numerical examples are presented to demonstrate the applicability of the algorithm.

Adaptive Path-Integral Autoencoder: Representation Learning and Planning for Dynamical Systems

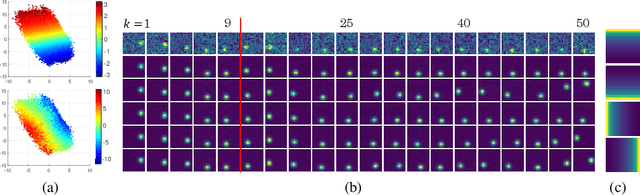
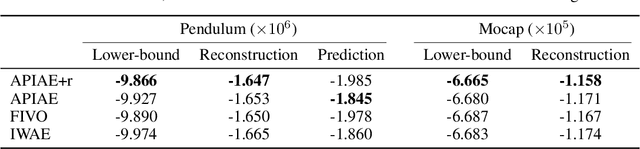
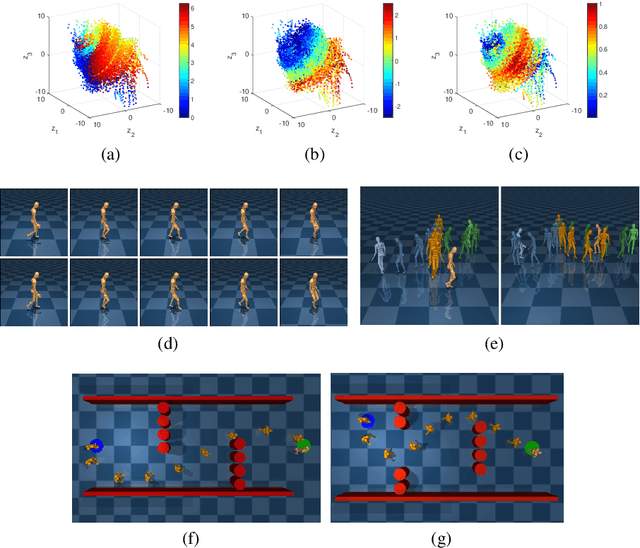
We present a representation learning algorithm that learns a low-dimensional latent dynamical system from high-dimensional \textit{sequential} raw data, e.g., video. The framework builds upon recent advances in amortized inference methods that use both an inference network and a refinement procedure to output samples from a variational distribution given an observation sequence, and takes advantage of the duality between control and inference to approximately solve the intractable inference problem using the path integral control approach. The learned dynamical model can be used to predict and plan the future states; we also present the efficient planning method that exploits the learned low-dimensional latent dynamics. Numerical experiments show that the proposed path-integral control based variational inference method leads to tighter lower bounds in statistical model learning of sequential data. The supplementary video: https://youtu.be/xCp35crUoLQ

Topology-Guided Path Integral Approach for Stochastic Optimal Control in Cluttered Environment

This paper addresses planning and control of robot motion under uncertainty that is formulated as a continuous-time, continuous-space stochastic optimal control problem, by developing a topology-guided path integral control method. The path integral control framework, which forms the backbone of the proposed method, re-writes the Hamilton-Jacobi-Bellman equation as a statistical inference problem; the resulting inference problem is solved by a sampling procedure that computes the distribution of controlled trajectories around the trajectory by the passive dynamics. For motion control of robots in a highly cluttered environment, however, this sampling can easily be trapped in a local minimum unless the sample size is very large, since the global optimality of local minima depends on the degree of uncertainty. Thus, a homology-embedded sampling-based planner that identifies many (potentially) local-minimum trajectories in different homology classes is developed to aid the sampling process. In combination with a receding-horizon fashion of the optimal control the proposed method produces a dynamically feasible and collision-free motion plans without being trapped in a local minimum. Numerical examples on a synthetic toy problem and on quadrotor control in a complex obstacle field demonstrate the validity of the proposed method.