Computing Melodic Templates in Oral Music Traditions

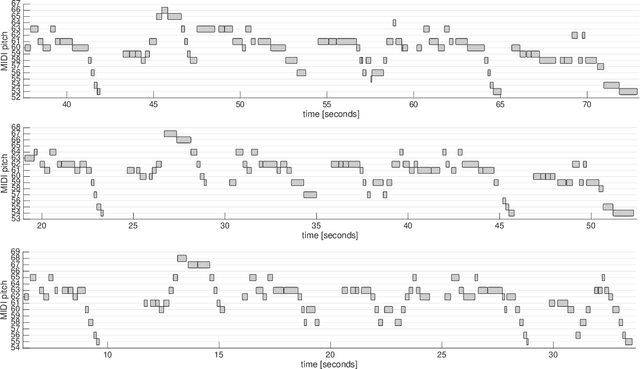
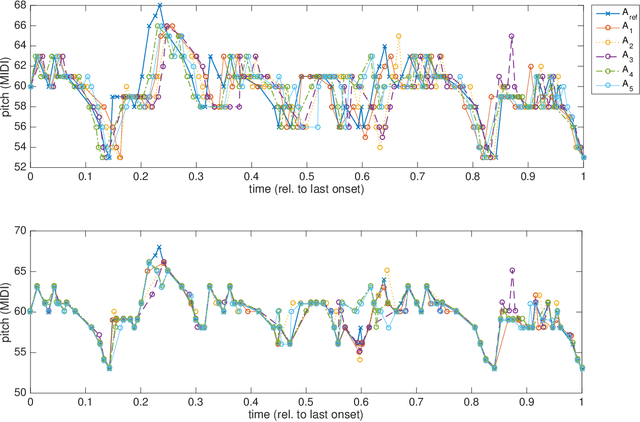
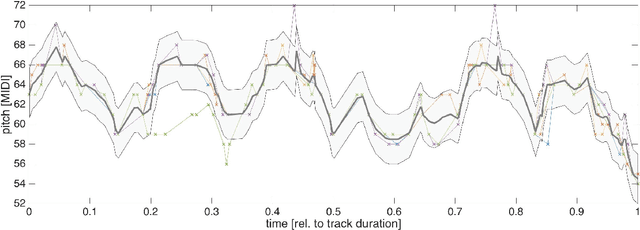
The term melodic template or skeleton refers to a basic melody which is subject to variation during a music performance. In many oral music tradition, these templates are implicitly passed throughout generations without ever being formalized in a score. In this work, we introduce a new geometric optimization problem, the spanning tube problem, to approximate a melodic template for a set of labeled performance transcriptions corresponding to an specific style in oral music traditions. Given a set of $n$ piecewise linear functions, we solve the problem of finding a continuous function, $f^*$, and a minimum value, $\varepsilon^*$, such that, the vertical segment of length $2\varepsilon^*$ centered at $(x,f^*(x))$ intersects at least $p$ functions ($p\leq n$). The method explored here also provide a novel tool for quantitatively assess the amount of melodic variation which occurs across performances.

Maths, Computation and Flamenco: overview and challenges

Flamenco is a rich performance-oriented art music genre from Southern Spain which attracts a growing community of aficionados around the globe. Due to its improvisational and expressive nature, its unique musical characteristics, and the fact that the genre is largely undocumented, flamenco poses a number of interesting mathematical and computational challenges. Most existing approaches in Musical Information Retrieval (MIR) were developed in the context of popular or classical music and do often not generalize well to non-Western music traditions, in particular when the underlying music theoretical assumptions do not hold for these genres. Over the recent decade, a number of computational problems related to the automatic analysis of flamenco music have been defined and several methods addressing a variety of musical aspects have been proposed. This paper provides an overview of the challenges which arise in the context of computational analysis of flamenco music and outlines an overview of existing approaches.

Kinodynamic Planning for an Energy-Efficient Autonomous Ornithopter

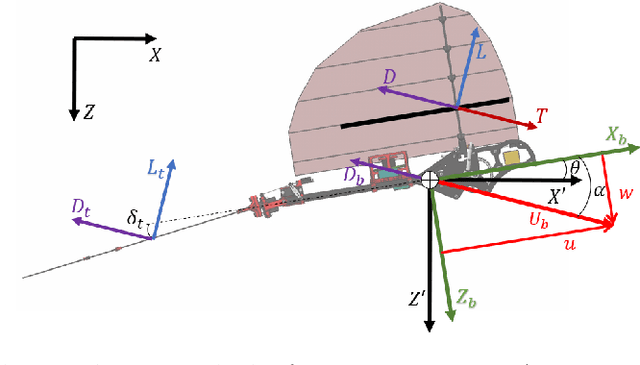
This paper presents a novel algorithm to plan energy-efficient trajectories for autonomous ornithopters. In general, trajectory optimization is quite a relevant problem for practical applications with \emph{Unmanned Aerial Vehicles} (UAVs). Even though the problem has been well studied for fixed and rotatory-wing vehicles, there are far fewer works exploring it for flapping-wing UAVs like ornithopters. These are of interest for many applications where long flight endurance, but also hovering capabilities are required. We propose an efficient approach to plan ornithopter trajectories that minimize energy consumption by combining gliding and flapping maneuvers. Our algorithm builds a tree of dynamically feasible trajectories and applies heuristic search for efficient online planning, using reference curves to guide the search and prune states. We present computational experiments to analyze and tune key parameters, as well as a comparison against a recent alternative probabilistic planning, showing best performance. Finally, we demonstrate how our algorithm can be used for planning perching maneuvers online.

Autonomous Planning for Multiple Aerial Cinematographers

This paper proposes a planning algorithm for autonomous media production with multiple Unmanned Aerial Vehicles (UAVs) in outdoor events. Given filming tasks specified by a media Director, we formulate an optimization problem to maximize the filming time considering battery constraints. As we conjecture that the problem is NP-hard, we consider a discretization version, and propose a graph-based algorithm that can find an optimal solution of the discrete problem for a single UAV in polynomial time. Then, a greedy strategy is applied to solve the problem sequentially for multiple UAVs. We demonstrate that our algorithm is efficient for small teams (3-5 UAVs) and that its performance is close to the optimum. We showcase our system in field experiments carrying out actual media production in an outdoor scenario with multiple UAVs.

Computing the $k$-resilience of a Synchronized Multi-Robot System

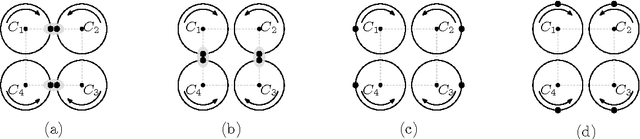
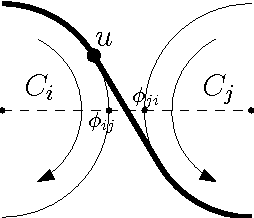
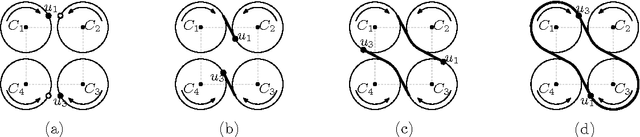
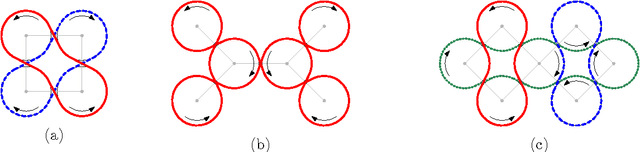
We study an optimization problem that arises in the design of covering strategies for multi-robot systems. Consider a team of $n$ cooperating robots traveling along predetermined closed and disjoint trajectories. Each robot needs to periodically communicate information to nearby robots. At places where two trajectories are within range of each other, a communication link is established, allowing two robots to exchange information, provided they are "synchronized", i.e., they visit the link at the same time. In this setting a communication graph is defined and a system of robots is called \emph{synchronized} if every pair of neighbors is synchronized. If one or more robots leave the system, then some trajectories are left unattended. To handle such cases in a synchronized system, when a live robot arrives to a communication link and detects the absence of the neighbor, it shifts to the neighboring trajectory to assume the unattended task. If enough robots leave, it may occur that a live robot enters a state of \emph{starvation}, failing to permanently meet other robots during flight. To measure the tolerance of the system under this phenomenon we define the \emph{$k$-resilience} as the minimum number of robots whose removal may cause $k$ surviving robots to enter a state of starvation. We show that the problem of computing the $k$-resilience is NP-hard if $k$ is part of the input, even if the communication graph is a tree. We propose algorithms to compute the $k$-resilience for constant values of $k$ in general communication graphs and show more efficient algorithms for systems whose communication graph is a tree.