Sergey Bereg
Computing Melodic Templates in Oral Music Traditions
Sep 27, 2022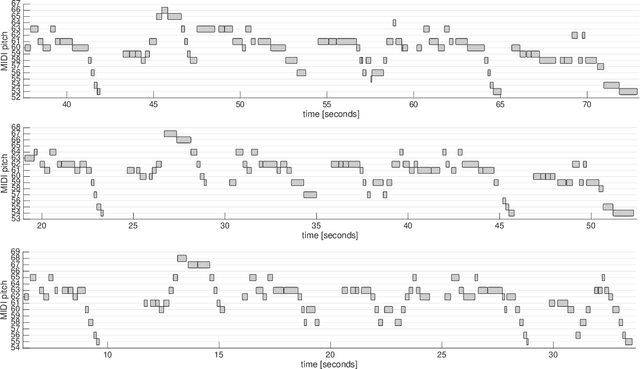
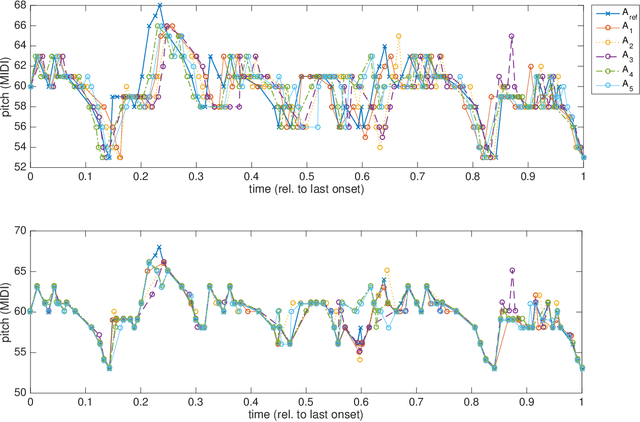

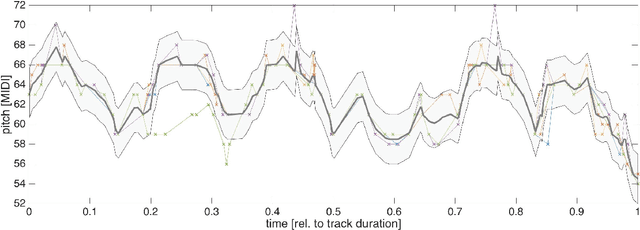
Abstract:The term melodic template or skeleton refers to a basic melody which is subject to variation during a music performance. In many oral music tradition, these templates are implicitly passed throughout generations without ever being formalized in a score. In this work, we introduce a new geometric optimization problem, the spanning tube problem, to approximate a melodic template for a set of labeled performance transcriptions corresponding to an specific style in oral music traditions. Given a set of $n$ piecewise linear functions, we solve the problem of finding a continuous function, $f^*$, and a minimum value, $\varepsilon^*$, such that, the vertical segment of length $2\varepsilon^*$ centered at $(x,f^*(x))$ intersects at least $p$ functions ($p\leq n$). The method explored here also provide a novel tool for quantitatively assess the amount of melodic variation which occurs across performances.
Efficient inspection of underground galleries using k robots with limited energy
Sep 21, 2022Abstract:We study the problem of optimally inspecting an underground (underwater) gallery with k agents. We consider a gallery with a single opening and with a tree topology rooted at the opening. Due to the small diameter of the pipes (caves), the agents are small robots with limited autonomy and there is a supply station at the gallery's opening. Therefore, they are initially placed at the root and periodically need to return to the supply station. Our goal is to design off-line strategies to efficiently cover the tree with $k$ small robots. We consider two objective functions: the covering time (maximum collective time) and the covering distance (total traveled distance). The maximum collective time is the maximum time spent by a robot needs to finish its assigned task (assuming that all the robots start at the same time); the total traveled distance is the sum of the lengths of all the covering walks. Since the problems are intractable for big trees, we propose approximation algorithms. Both efficiency and accuracy of the suboptimal solutions are empirically showed for random trees through intensive numerical experiments.
Computing the $k$-resilience of a Synchronized Multi-Robot System
Jul 22, 2017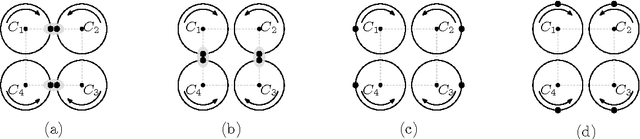
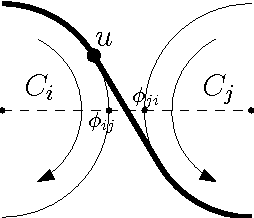
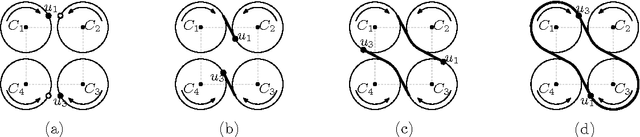
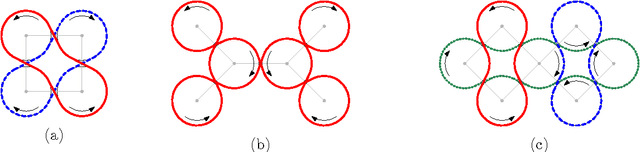
Abstract:We study an optimization problem that arises in the design of covering strategies for multi-robot systems. Consider a team of $n$ cooperating robots traveling along predetermined closed and disjoint trajectories. Each robot needs to periodically communicate information to nearby robots. At places where two trajectories are within range of each other, a communication link is established, allowing two robots to exchange information, provided they are "synchronized", i.e., they visit the link at the same time. In this setting a communication graph is defined and a system of robots is called \emph{synchronized} if every pair of neighbors is synchronized. If one or more robots leave the system, then some trajectories are left unattended. To handle such cases in a synchronized system, when a live robot arrives to a communication link and detects the absence of the neighbor, it shifts to the neighboring trajectory to assume the unattended task. If enough robots leave, it may occur that a live robot enters a state of \emph{starvation}, failing to permanently meet other robots during flight. To measure the tolerance of the system under this phenomenon we define the \emph{$k$-resilience} as the minimum number of robots whose removal may cause $k$ surviving robots to enter a state of starvation. We show that the problem of computing the $k$-resilience is NP-hard if $k$ is part of the input, even if the communication graph is a tree. We propose algorithms to compute the $k$-resilience for constant values of $k$ in general communication graphs and show more efficient algorithms for systems whose communication graph is a tree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge