Computing the $k$-resilience of a Synchronized Multi-Robot System
Paper and Code
Jul 22, 2017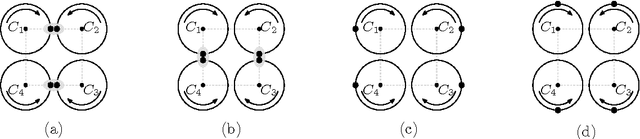
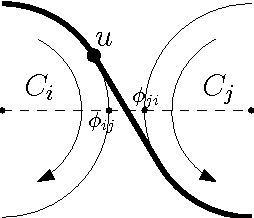
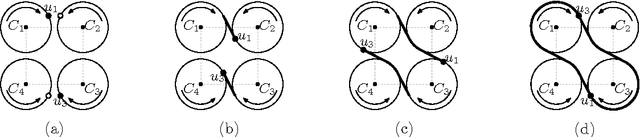
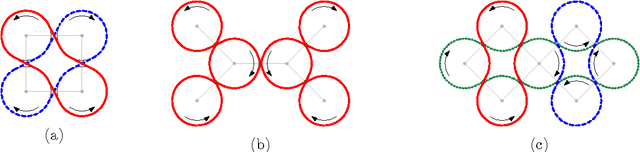
We study an optimization problem that arises in the design of covering strategies for multi-robot systems. Consider a team of $n$ cooperating robots traveling along predetermined closed and disjoint trajectories. Each robot needs to periodically communicate information to nearby robots. At places where two trajectories are within range of each other, a communication link is established, allowing two robots to exchange information, provided they are "synchronized", i.e., they visit the link at the same time. In this setting a communication graph is defined and a system of robots is called \emph{synchronized} if every pair of neighbors is synchronized. If one or more robots leave the system, then some trajectories are left unattended. To handle such cases in a synchronized system, when a live robot arrives to a communication link and detects the absence of the neighbor, it shifts to the neighboring trajectory to assume the unattended task. If enough robots leave, it may occur that a live robot enters a state of \emph{starvation}, failing to permanently meet other robots during flight. To measure the tolerance of the system under this phenomenon we define the \emph{$k$-resilience} as the minimum number of robots whose removal may cause $k$ surviving robots to enter a state of starvation. We show that the problem of computing the $k$-resilience is NP-hard if $k$ is part of the input, even if the communication graph is a tree. We propose algorithms to compute the $k$-resilience for constant values of $k$ in general communication graphs and show more efficient algorithms for systems whose communication graph is a tree.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge