High-Accuracy Machine Learning Techniques for Functional Connectome Fingerprinting and Cognitive State Decoding

The human brain is a complex network comprised of functionally and anatomically interconnected brain regions. A growing number of studies have suggested that empirical estimates of brain networks may be useful for discovery of biomarkers of disease and cognitive state. A prerequisite for realizing this aim, however, is that brain networks also serve as reliable markers of an individual. Here, using Human Connectome Project data, we build upon recent studies examining brain-based fingerprints of individual subjects and cognitive states based on cognitively-demanding tasks that assess, for example, working memory, theory of mind, and motor function. Our approach achieves accuracy of up to 99\% for both identification of the subject of an fMRI scan, and for classification of the cognitive state of a previously-unseen subject in a scan. More broadly, we explore the accuracy and reliability of five different machine learning techniques on subject fingerprinting and cognitive state decoding objectives, using functional connectivity data from fMRI scans of a high number of subjects (865) across a number of cognitive states (8). These results represent an advance on existing techniques for functional connectivity-based brain fingerprinting and state decoding. Additionally, 16 different pre-processing pipelines are compared in order to characterize the effects of different aspects of the production of functional connectomes (FCs) on the accuracy of subject and task classification, and to identify possible confounds.

Computing the $k$-resilience of a Synchronized Multi-Robot System

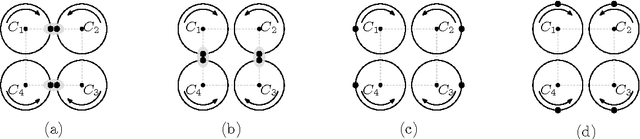
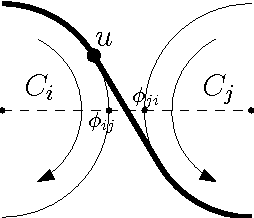
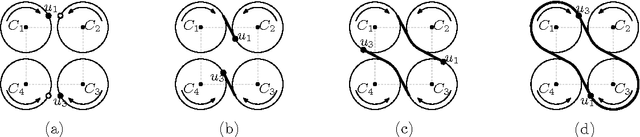
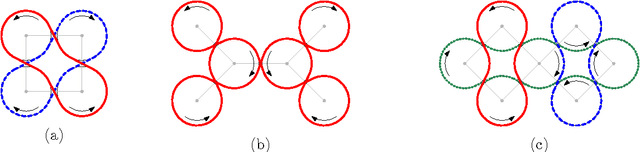
We study an optimization problem that arises in the design of covering strategies for multi-robot systems. Consider a team of $n$ cooperating robots traveling along predetermined closed and disjoint trajectories. Each robot needs to periodically communicate information to nearby robots. At places where two trajectories are within range of each other, a communication link is established, allowing two robots to exchange information, provided they are "synchronized", i.e., they visit the link at the same time. In this setting a communication graph is defined and a system of robots is called \emph{synchronized} if every pair of neighbors is synchronized. If one or more robots leave the system, then some trajectories are left unattended. To handle such cases in a synchronized system, when a live robot arrives to a communication link and detects the absence of the neighbor, it shifts to the neighboring trajectory to assume the unattended task. If enough robots leave, it may occur that a live robot enters a state of \emph{starvation}, failing to permanently meet other robots during flight. To measure the tolerance of the system under this phenomenon we define the \emph{$k$-resilience} as the minimum number of robots whose removal may cause $k$ surviving robots to enter a state of starvation. We show that the problem of computing the $k$-resilience is NP-hard if $k$ is part of the input, even if the communication graph is a tree. We propose algorithms to compute the $k$-resilience for constant values of $k$ in general communication graphs and show more efficient algorithms for systems whose communication graph is a tree.