Autonomous Planning for Multiple Aerial Cinematographers

This paper proposes a planning algorithm for autonomous media production with multiple Unmanned Aerial Vehicles (UAVs) in outdoor events. Given filming tasks specified by a media Director, we formulate an optimization problem to maximize the filming time considering battery constraints. As we conjecture that the problem is NP-hard, we consider a discretization version, and propose a graph-based algorithm that can find an optimal solution of the discrete problem for a single UAV in polynomial time. Then, a greedy strategy is applied to solve the problem sequentially for multiple UAVs. We demonstrate that our algorithm is efficient for small teams (3-5 UAVs) and that its performance is close to the optimum. We showcase our system in field experiments carrying out actual media production in an outdoor scenario with multiple UAVs.

Computing the $k$-resilience of a Synchronized Multi-Robot System

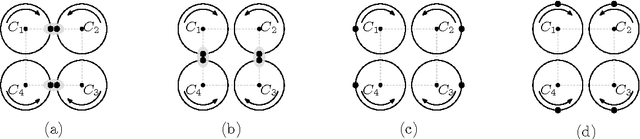
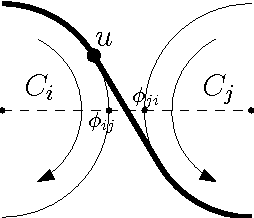
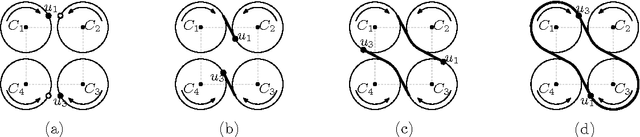
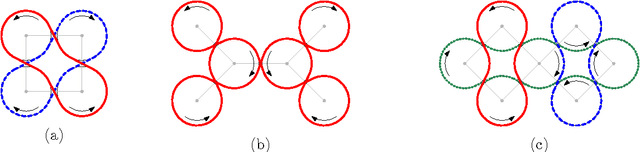
We study an optimization problem that arises in the design of covering strategies for multi-robot systems. Consider a team of $n$ cooperating robots traveling along predetermined closed and disjoint trajectories. Each robot needs to periodically communicate information to nearby robots. At places where two trajectories are within range of each other, a communication link is established, allowing two robots to exchange information, provided they are "synchronized", i.e., they visit the link at the same time. In this setting a communication graph is defined and a system of robots is called \emph{synchronized} if every pair of neighbors is synchronized. If one or more robots leave the system, then some trajectories are left unattended. To handle such cases in a synchronized system, when a live robot arrives to a communication link and detects the absence of the neighbor, it shifts to the neighboring trajectory to assume the unattended task. If enough robots leave, it may occur that a live robot enters a state of \emph{starvation}, failing to permanently meet other robots during flight. To measure the tolerance of the system under this phenomenon we define the \emph{$k$-resilience} as the minimum number of robots whose removal may cause $k$ surviving robots to enter a state of starvation. We show that the problem of computing the $k$-resilience is NP-hard if $k$ is part of the input, even if the communication graph is a tree. We propose algorithms to compute the $k$-resilience for constant values of $k$ in general communication graphs and show more efficient algorithms for systems whose communication graph is a tree.