An efficient strategy for path planning with a tethered marsupial robotics system

A marsupial robotics system comprises three components: an Unmanned Ground Vehicle (UGV), an Unmanned Aerial Vehicle (UAV), and a tether connecting both robots. Marsupial systems are highly beneficial in industry as they extend the UAV's battery life during flight. This paper introduces a novel strategy for a specific path planning problem in marsupial systems, where each of the components must avoid collisions with ground and aerial obstacles modeled as 3D cuboids. Given an initial configuration in which the UAV is positioned atop the UGV, the goal is to reach an aerial target with the UAV. We assume that the UGV first moves to a position from which the UAV can take off and fly through a vertical plane to reach an aerial target. We propose an approach that discretizes the space to approximate an optimal solution, minimizing the sum of the lengths of the ground and air paths. First, we assume a taut tether and use a novel algorithm that leverages the convexity of the tether and the geometry of obstacles to efficiently determine the locus of feasible take-off points for the UAV. We then apply this result to scenarios that involve loose tethers. The simulation test results show that our approach can solve complex situations in seconds, outperforming a baseline planning algorithm based on RRT* (Rapidly exploring Random Trees).

Computing Melodic Templates in Oral Music Traditions

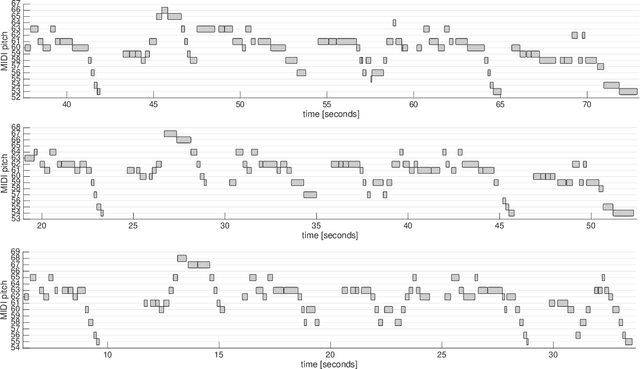
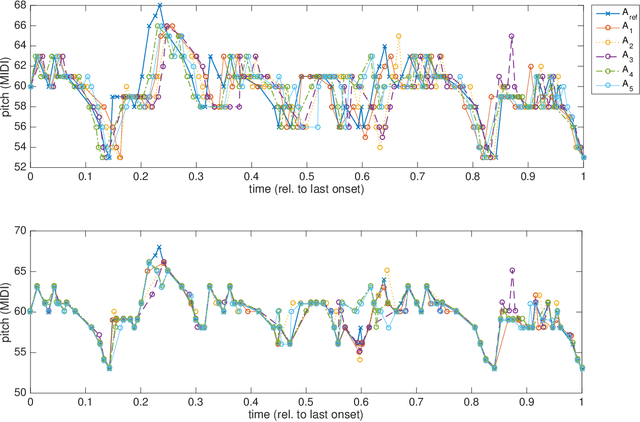
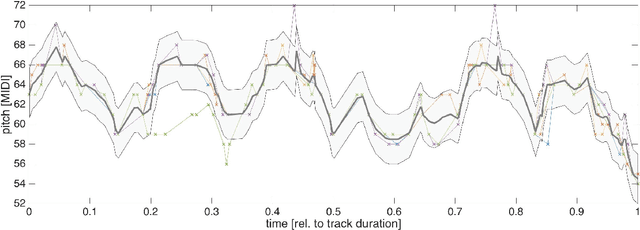
The term melodic template or skeleton refers to a basic melody which is subject to variation during a music performance. In many oral music tradition, these templates are implicitly passed throughout generations without ever being formalized in a score. In this work, we introduce a new geometric optimization problem, the spanning tube problem, to approximate a melodic template for a set of labeled performance transcriptions corresponding to an specific style in oral music traditions. Given a set of $n$ piecewise linear functions, we solve the problem of finding a continuous function, $f^*$, and a minimum value, $\varepsilon^*$, such that, the vertical segment of length $2\varepsilon^*$ centered at $(x,f^*(x))$ intersects at least $p$ functions ($p\leq n$). The method explored here also provide a novel tool for quantitatively assess the amount of melodic variation which occurs across performances.

Scaling and compressing melodies using geometric similarity measures

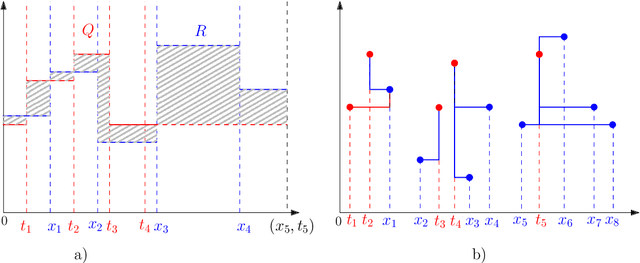
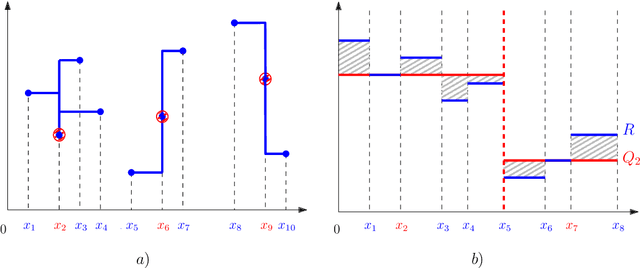
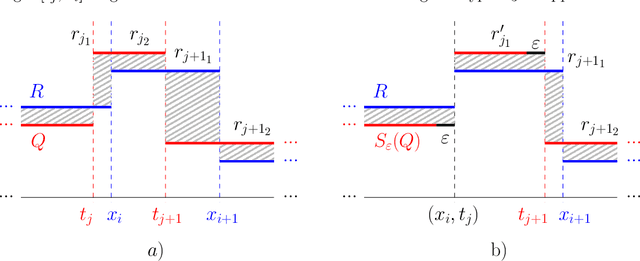
Melodic similarity measurement is of key importance in music information retrieval. In this paper, we use geometric matching techniques to measure the similarity between two melodies. We represent music as sets of points or sets of horizontal line segments in the Euclidean plane and propose efficient algorithms for optimization problems inspired in two operations on melodies; linear scaling and audio compression. In the scaling problem, an incoming query melody is scaled forward until the similarity measure between the query and a reference melody is minimized. The compression problem asks for a subset of notes of a given melody such that the matching cost between the selected notes and the reference melody is minimized.