Computing Melodic Templates in Oral Music Traditions
Paper and Code
Sep 27, 2022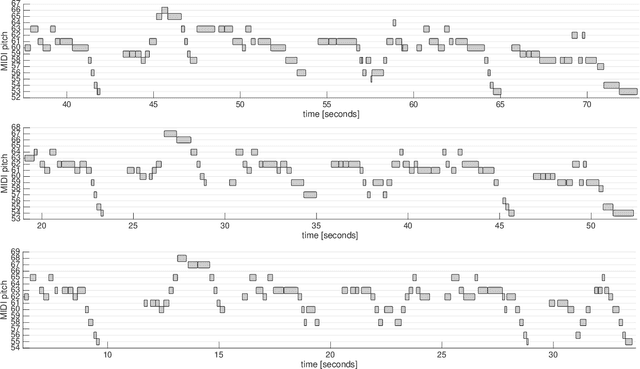
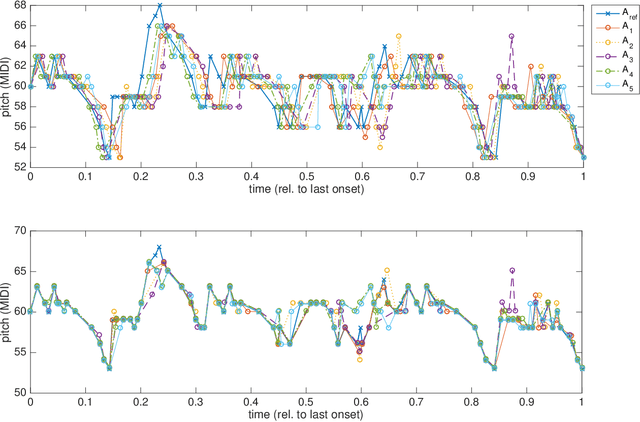

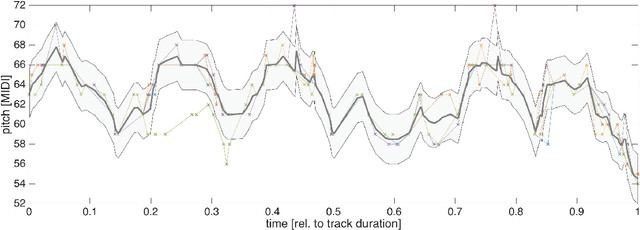
The term melodic template or skeleton refers to a basic melody which is subject to variation during a music performance. In many oral music tradition, these templates are implicitly passed throughout generations without ever being formalized in a score. In this work, we introduce a new geometric optimization problem, the spanning tube problem, to approximate a melodic template for a set of labeled performance transcriptions corresponding to an specific style in oral music traditions. Given a set of $n$ piecewise linear functions, we solve the problem of finding a continuous function, $f^*$, and a minimum value, $\varepsilon^*$, such that, the vertical segment of length $2\varepsilon^*$ centered at $(x,f^*(x))$ intersects at least $p$ functions ($p\leq n$). The method explored here also provide a novel tool for quantitatively assess the amount of melodic variation which occurs across performances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge