Talaria: Interactively Optimizing Machine Learning Models for Efficient Inference

On-device machine learning (ML) moves computation from the cloud to personal devices, protecting user privacy and enabling intelligent user experiences. However, fitting models on devices with limited resources presents a major technical challenge: practitioners need to optimize models and balance hardware metrics such as model size, latency, and power. To help practitioners create efficient ML models, we designed and developed Talaria: a model visualization and optimization system. Talaria enables practitioners to compile models to hardware, interactively visualize model statistics, and simulate optimizations to test the impact on inference metrics. Since its internal deployment two years ago, we have evaluated Talaria using three methodologies: (1) a log analysis highlighting its growth of 800+ practitioners submitting 3,600+ models; (2) a usability survey with 26 users assessing the utility of 20 Talaria features; and (3) a qualitative interview with the 7 most active users about their experience using Talaria.

Neo: Generalizing Confusion Matrix Visualization to Hierarchical and Multi-Output Labels

The confusion matrix, a ubiquitous visualization for helping people evaluate machine learning models, is a tabular layout that compares predicted class labels against actual class labels over all data instances. We conduct formative research with machine learning practitioners at a large technology company and find that conventional confusion matrices do not support more complex data-structures found in modern-day applications, such as hierarchical and multi-output labels. To express such variations of confusion matrices, we design an algebra that models confusion matrices as probability distributions. Based on this algebra, we develop Neo, a visual analytics system that enables practitioners to flexibly author and interact with hierarchical and multi-output confusion matrices, visualize derived metrics, renormalize confusions, and share matrix specifications. Finally, we demonstrate Neo's utility with three case studies that help people better understand model performance and reveal hidden confusions.

Uncertainty-Aware Principal Component Analysis

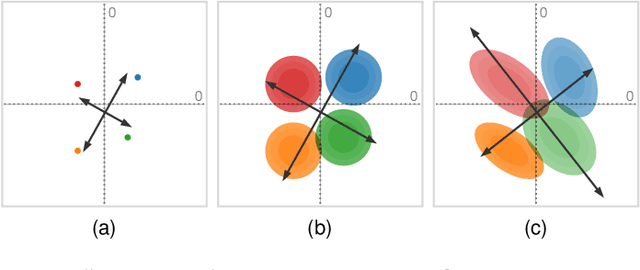
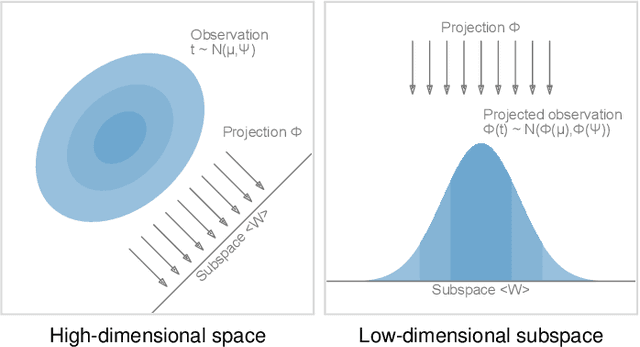
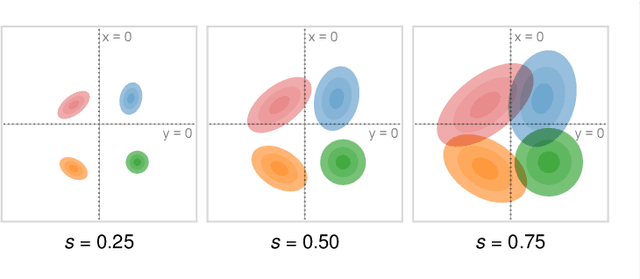
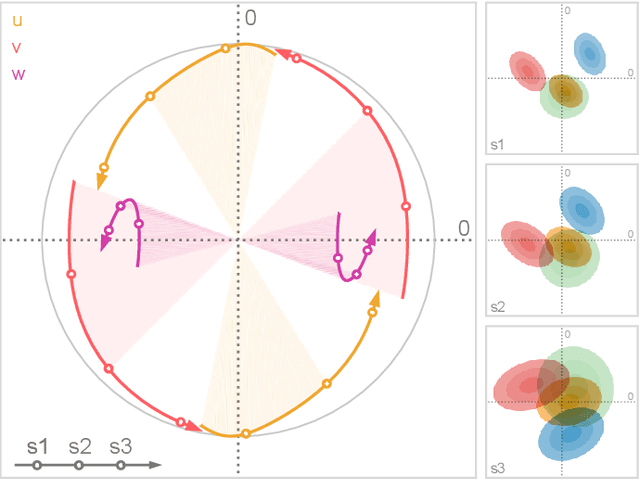
We present a technique to perform dimensionality reduction on data that is subject to uncertainty. Our method is a generalization of traditional principal component analysis (PCA) to multivariate probability distributions. In comparison to non-linear methods, linear dimensionality reduction techniques have the advantage that the characteristics of such probability distributions remain intact after projection. We derive a representation of the covariance matrix that respects potential uncertainty in each of the observations, building the mathematical foundation of our new method uncertainty-aware PCA. In addition to the accuracy and performance gained by our approach over sampling-based strategies, our formulation allows us to perform sensitivity analysis with regard to the uncertainty in the data. For this, we propose factor traces as a novel visualization that enables us to better understand the influence of uncertainty on the chosen principal components. We provide multiple examples of our technique using real-world datasets and show how to propagate multivariate normal distributions through PCA in closed-form. Furthermore, we discuss extensions and limitations of our approach.