Uncertainty-Aware Principal Component Analysis
Paper and Code
May 03, 2019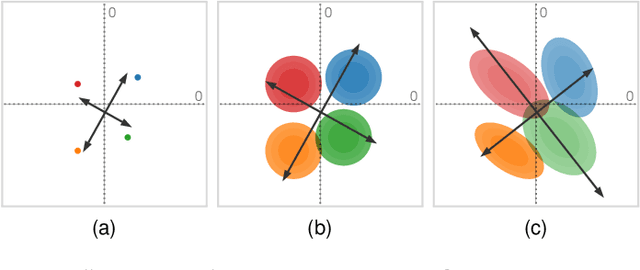
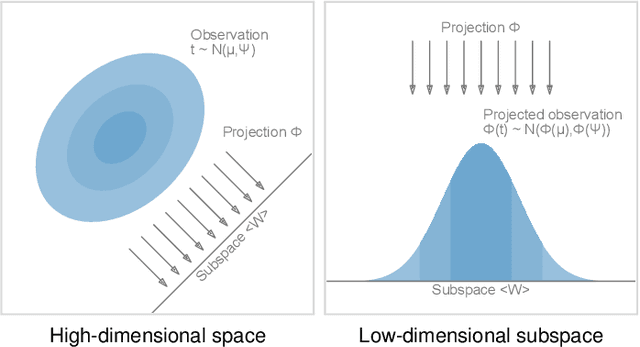
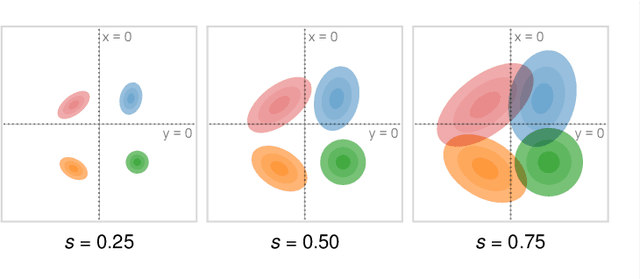
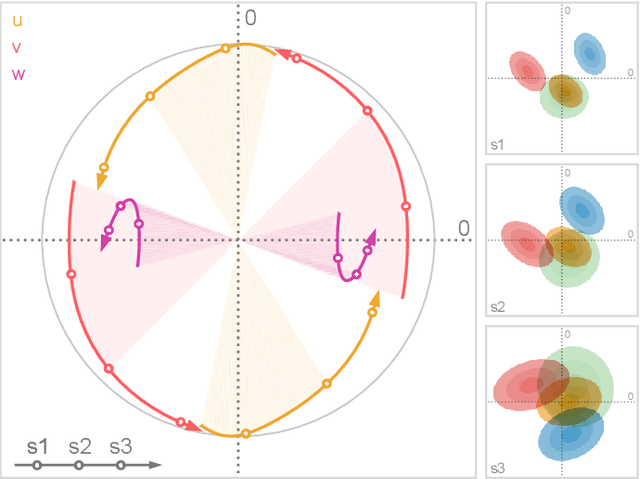
We present a technique to perform dimensionality reduction on data that is subject to uncertainty. Our method is a generalization of traditional principal component analysis (PCA) to multivariate probability distributions. In comparison to non-linear methods, linear dimensionality reduction techniques have the advantage that the characteristics of such probability distributions remain intact after projection. We derive a representation of the covariance matrix that respects potential uncertainty in each of the observations, building the mathematical foundation of our new method uncertainty-aware PCA. In addition to the accuracy and performance gained by our approach over sampling-based strategies, our formulation allows us to perform sensitivity analysis with regard to the uncertainty in the data. For this, we propose factor traces as a novel visualization that enables us to better understand the influence of uncertainty on the chosen principal components. We provide multiple examples of our technique using real-world datasets and show how to propagate multivariate normal distributions through PCA in closed-form. Furthermore, we discuss extensions and limitations of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge