Machine Learning-Driven Student Performance Prediction for Enhancing Tiered Instruction

Student performance prediction is one of the most important subjects in educational data mining. As a modern technology, machine learning offers powerful capabilities in feature extraction and data modeling, providing essential support for diverse application scenarios, as evidenced by recent studies confirming its effectiveness in educational data mining. However, despite extensive prediction experiments, machine learning methods have not been effectively integrated into practical teaching strategies, hindering their application in modern education. In addition, massive features as input variables for machine learning algorithms often leads to information redundancy, which can negatively impact prediction accuracy. Therefore, how to effectively use machine learning methods to predict student performance and integrate the prediction results with actual teaching scenarios is a worthy research subject. To this end, this study integrates the results of machine learning-based student performance prediction with tiered instruction, aiming to enhance student outcomes in target course, which is significant for the application of educational data mining in contemporary teaching scenarios. Specifically, we collect original educational data and perform feature selection to reduce information redundancy. Then, the performance of five representative machine learning methods is analyzed and discussed with Random Forest showing the best performance. Furthermore, based on the results of the classification of students, tiered instruction is applied accordingly, and different teaching objectives and contents are set for all levels of students. The comparison of teaching outcomes between the control and experimental classes, along with the analysis of questionnaire results, demonstrates the effectiveness of the proposed framework.

Improving DNN Fault Tolerance using Weight Pruning and Differential Crossbar Mapping for ReRAM-based Edge AI

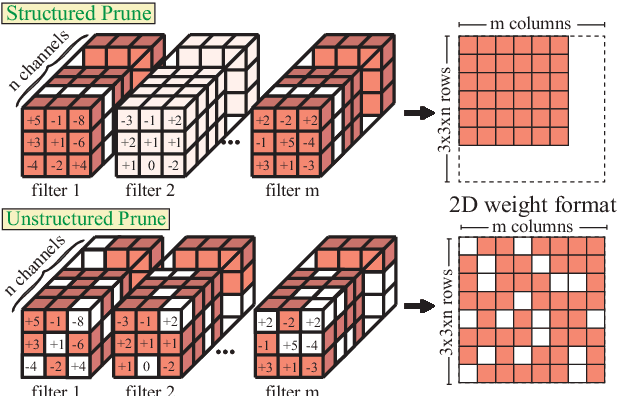
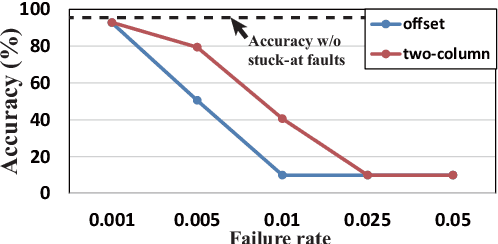
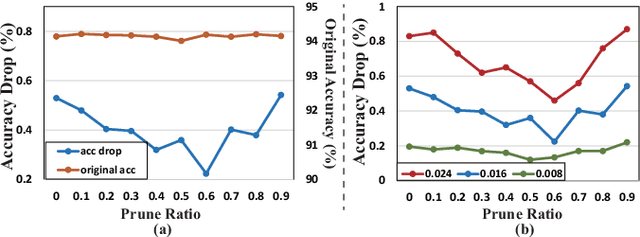
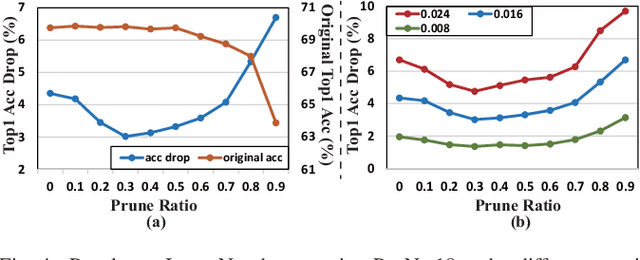
Recent research demonstrated the promise of using resistive random access memory (ReRAM) as an emerging technology to perform inherently parallel analog domain in-situ matrix-vector multiplication -- the intensive and key computation in deep neural networks (DNNs). However, hardware failure, such as stuck-at-fault defects, is one of the main concerns that impedes the ReRAM devices to be a feasible solution for real implementations. The existing solutions to address this issue usually require an optimization to be conducted for each individual device, which is impractical for mass-produced products (e.g., IoT devices). In this paper, we rethink the value of weight pruning in ReRAM-based DNN design from the perspective of model fault tolerance. And a differential mapping scheme is proposed to improve the fault tolerance under a high stuck-on fault rate. Our method can tolerate almost an order of magnitude higher failure rate than the traditional two-column method in representative DNN tasks. More importantly, our method does not require extra hardware cost compared to the traditional two-column mapping scheme. The improvement is universal and does not require the optimization process for each individual device.

Anomaly Detection with Tensor Networks

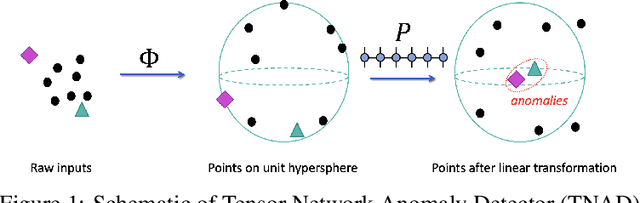
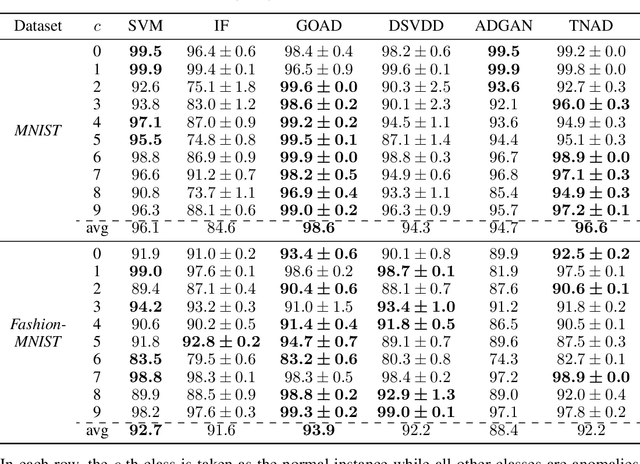
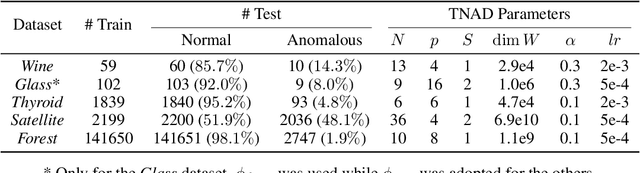
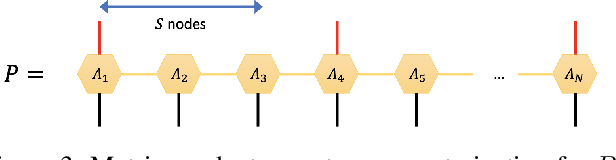
Originating from condensed matter physics, tensor networks are compact representations of high-dimensional tensors. In this paper, the prowess of tensor networks is demonstrated on the particular task of one-class anomaly detection. We exploit the memory and computational efficiency of tensor networks to learn a linear transformation over a space with dimension exponential in the number of original features. The linearity of our model enables us to ensure a tight fit around training instances by penalizing the model's global tendency to a predict normality via its Frobenius norm---a task that is infeasible for most deep learning models. Our method outperforms deep and classical algorithms on tabular datasets and produces competitive results on image datasets, despite not exploiting the locality of images.