Entanglement and Tensor Networks for Supervised Image Classification

Tensor networks, originally designed to address computational problems in quantum many-body physics, have recently been applied to machine learning tasks. However, compared to quantum physics, where the reasons for the success of tensor network approaches over the last 30 years is well understood, very little is yet known about why these techniques work for machine learning. The goal of this paper is to investigate entanglement properties of tensor network models in a current machine learning application, in order to uncover general principles that may guide future developments. We revisit the use of tensor networks for supervised image classification using the MNIST data set of handwritten digits, as pioneered by Stoudenmire and Schwab [Adv. in Neur. Inform. Proc. Sys. 29, 4799 (2016)]. Firstly we hypothesize about which state the tensor network might be learning during training. For that purpose, we propose a plausible candidate state $|\Sigma_{\ell}\rangle$ (built as a superposition of product states corresponding to images in the training set) and investigate its entanglement properties. We conclude that $|\Sigma_{\ell}\rangle$ is so robustly entangled that it cannot be approximated by the tensor network used in that work, which must therefore be representing a very different state. Secondly, we use tensor networks with a block product structure, in which entanglement is restricted within small blocks of $n \times n$ pixels/qubits. We find that these states are extremely expressive (e.g. training accuracy of $99.97 \%$ already for $n=2$), suggesting that long-range entanglement may not be essential for image classification. However, in our current implementation, optimization leads to over-fitting, resulting in test accuracies that are not competitive with other current approaches.

Anomaly Detection with Tensor Networks

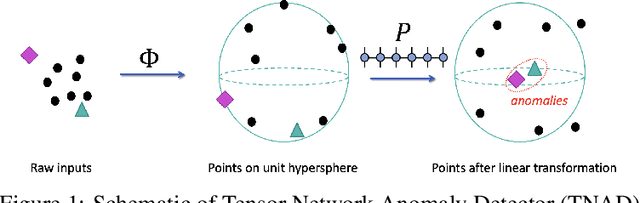
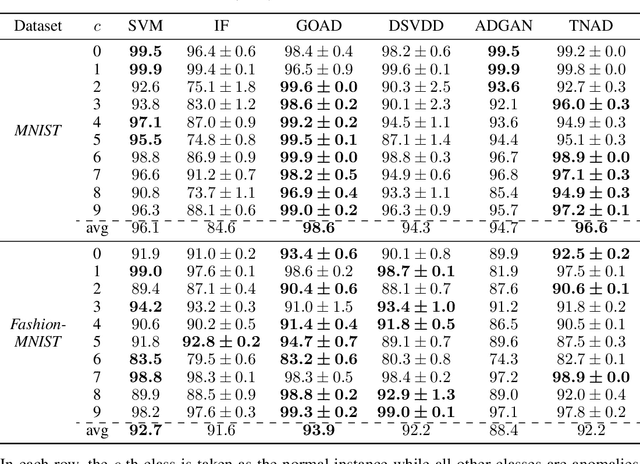
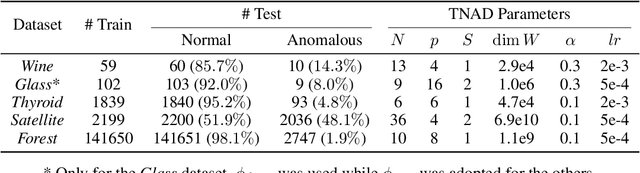
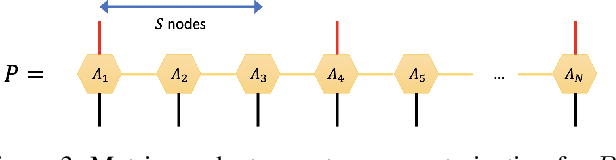
Originating from condensed matter physics, tensor networks are compact representations of high-dimensional tensors. In this paper, the prowess of tensor networks is demonstrated on the particular task of one-class anomaly detection. We exploit the memory and computational efficiency of tensor networks to learn a linear transformation over a space with dimension exponential in the number of original features. The linearity of our model enables us to ensure a tight fit around training instances by penalizing the model's global tendency to a predict normality via its Frobenius norm---a task that is infeasible for most deep learning models. Our method outperforms deep and classical algorithms on tabular datasets and produces competitive results on image datasets, despite not exploiting the locality of images.

TensorNetwork: A Library for Physics and Machine Learning

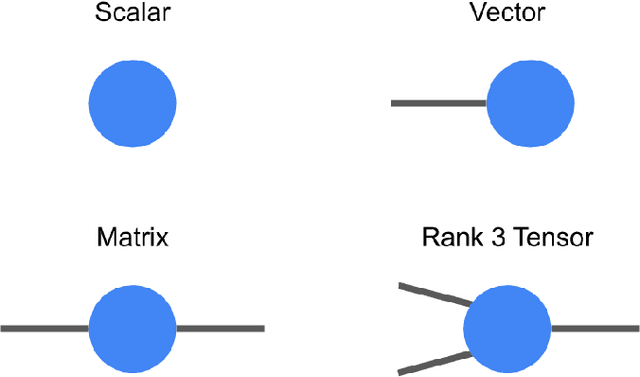
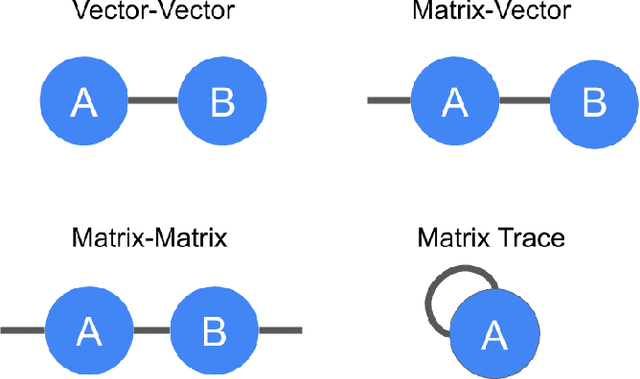
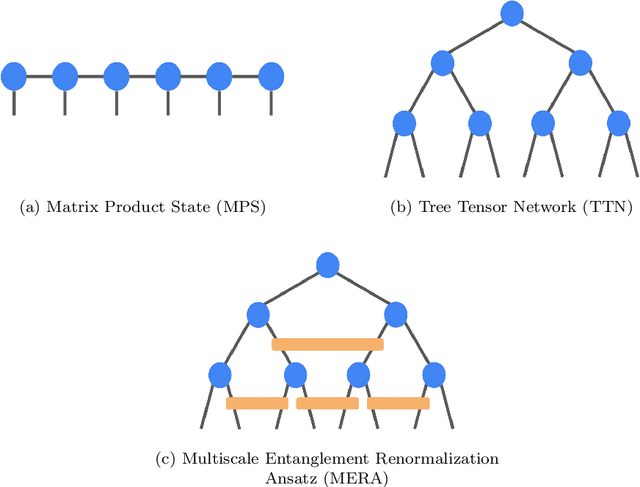
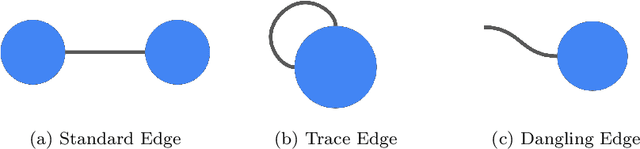
TensorNetwork is an open source library for implementing tensor network algorithms. Tensor networks are sparse data structures originally designed for simulating quantum many-body physics, but are currently also applied in a number of other research areas, including machine learning. We demonstrate the use of the API with applications both physics and machine learning, with details appearing in companion papers.

Arbitrary Discrete Sequence Anomaly Detection with Zero Boundary LSTM

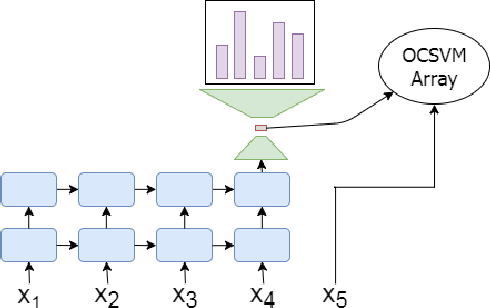
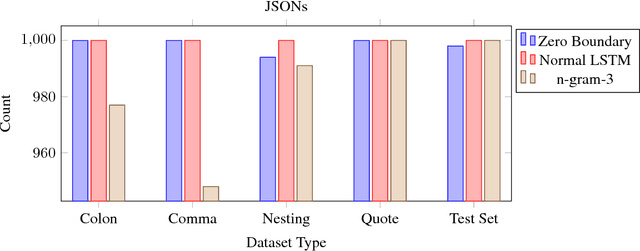
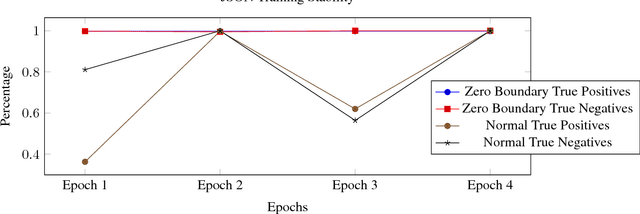
We propose a simple mathematical definition and new neural architecture for finding anomalies within discrete sequence datasets. Our model comprises of a modified LSTM autoencoder and an array of One-Class SVMs. The LSTM takes in elements from a sequence and creates context vectors that are used to predict the probability distribution of the following element. These context vectors are then used to train an array of One-Class SVMs. These SVMs are used to determine an outlier boundary in context space.We show that our method is consistently more stable and also outperforms standard LSTM and sliding window anomaly detection systems on two generated datasets.