Retentive Neural Quantum States: Efficient Ansätze for Ab Initio Quantum Chemistry

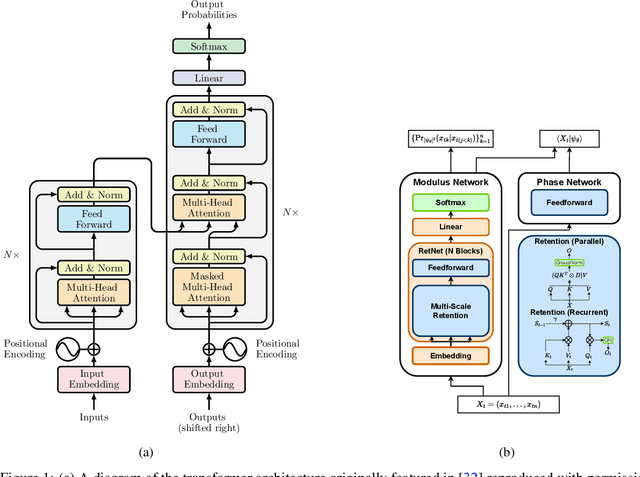
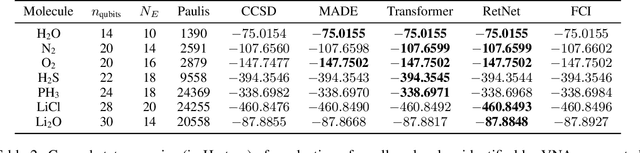
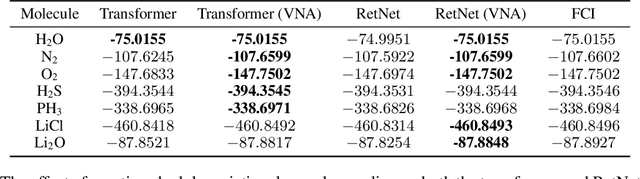
Neural-network quantum states (NQS) has emerged as a powerful application of quantum-inspired deep learning for variational Monte Carlo methods, offering a competitive alternative to existing techniques for identifying ground states of quantum problems. A significant advancement toward improving the practical scalability of NQS has been the incorporation of autoregressive models, most recently transformers, as variational ansatze. Transformers learn sequence information with greater expressiveness than recurrent models, but at the cost of increased time complexity with respect to sequence length. We explore the use of the retentive network (RetNet), a recurrent alternative to transformers, as an ansatz for solving electronic ground state problems in $\textit{ab initio}$ quantum chemistry. Unlike transformers, RetNets overcome this time complexity bottleneck by processing data in parallel during training, and recurrently during inference. We give a simple computational cost estimate of the RetNet and directly compare it with similar estimates for transformers, establishing a clear threshold ratio of problem-to-model size past which the RetNet's time complexity outperforms that of the transformer. Though this efficiency can comes at the expense of decreased expressiveness relative to the transformer, we overcome this gap through training strategies that leverage the autoregressive structure of the model -- namely, variational neural annealing. Our findings support the RetNet as a means of improving the time complexity of NQS without sacrificing accuracy. We provide further evidence that the ablative improvements of neural annealing extend beyond the RetNet architecture, suggesting it would serve as an effective general training strategy for autoregressive NQS.

LLM-initialized Differentiable Causal Discovery

The discovery of causal relationships between random variables is an important yet challenging problem that has applications across many scientific domains. Differentiable causal discovery (DCD) methods are effective in uncovering causal relationships from observational data; however, these approaches often suffer from limited interpretability and face challenges in incorporating domain-specific prior knowledge. In contrast, Large Language Models (LLMs)-based causal discovery approaches have recently been shown capable of providing useful priors for causal discovery but struggle with formal causal reasoning. In this paper, we propose LLM-DCD, which uses an LLM to initialize the optimization of the maximum likelihood objective function of DCD approaches, thereby incorporating strong priors into the discovery method. To achieve this initialization, we design our objective function to depend on an explicitly defined adjacency matrix of the causal graph as its only variational parameter. Directly optimizing the explicitly defined adjacency matrix provides a more interpretable approach to causal discovery. Additionally, we demonstrate higher accuracy on key benchmarking datasets of our approach compared to state-of-the-art alternatives, and provide empirical evidence that the quality of the initialization directly impacts the quality of the final output of our DCD approach. LLM-DCD opens up new opportunities for traditional causal discovery methods like DCD to benefit from future improvements in the causal reasoning capabilities of LLMs.

TensorNetwork on TensorFlow: A Spin Chain Application Using Tree Tensor Networks

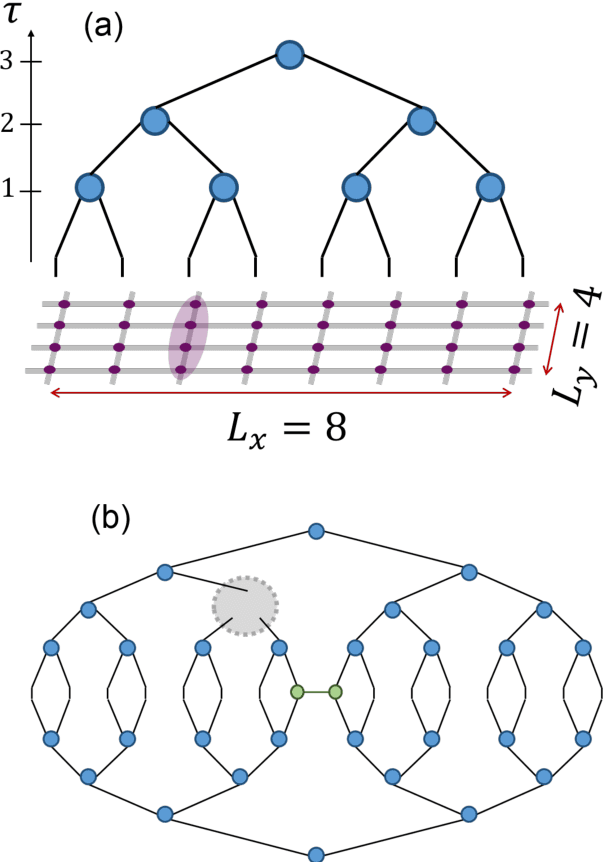
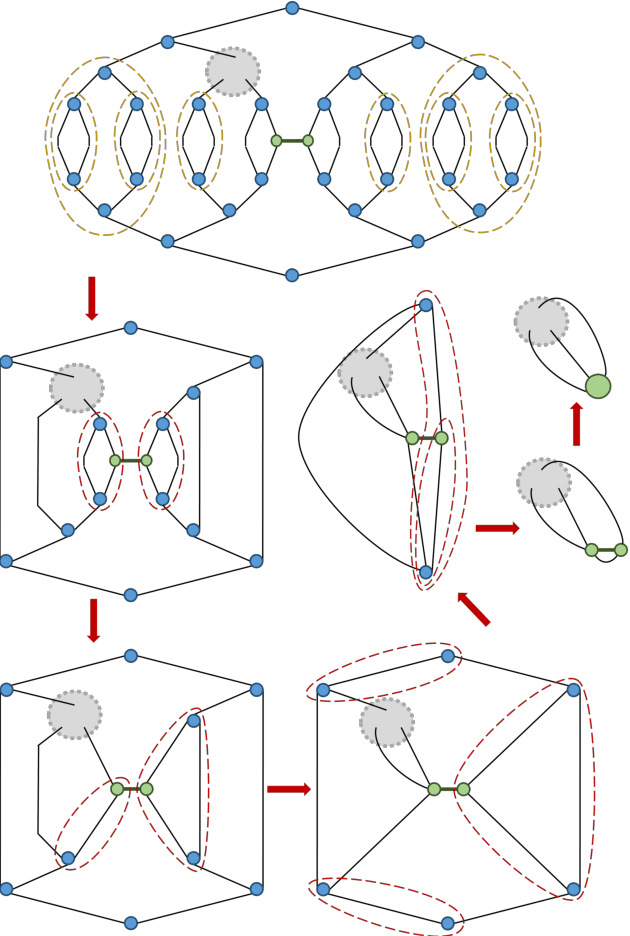
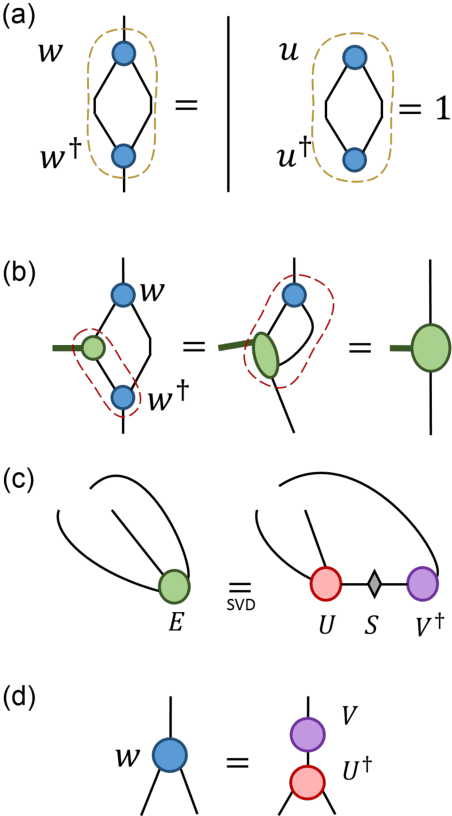
TensorNetwork is an open source library for implementing tensor network algorithms in TensorFlow. We describe a tree tensor network (TTN) algorithm for approximating the ground state of either a periodic quantum spin chain (1D) or a lattice model on a thin torus (2D), and implement the algorithm using TensorNetwork. We use a standard energy minimization procedure over a TTN ansatz with bond dimension $\chi$, with a computational cost that scales as $O(\chi^4)$. Using bond dimension $\chi \in [32,256]$ we compare the use of CPUs with GPUs and observe significant computational speed-ups, up to a factor of $100$, using a GPU and the TensorNetwork library.

TensorNetwork: A Library for Physics and Machine Learning

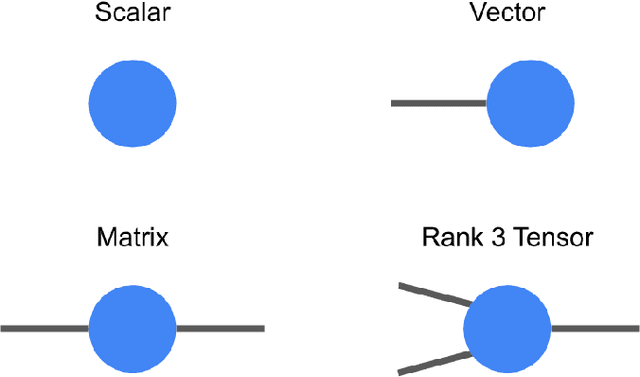
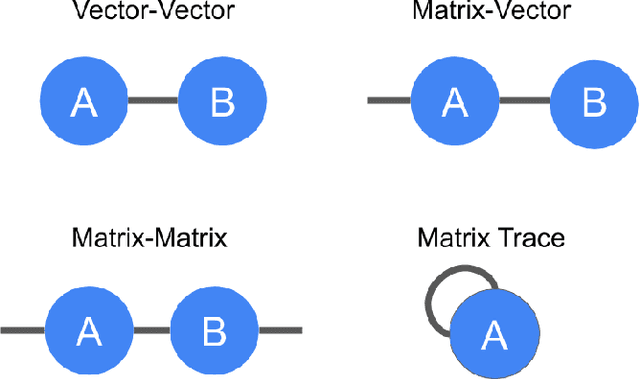
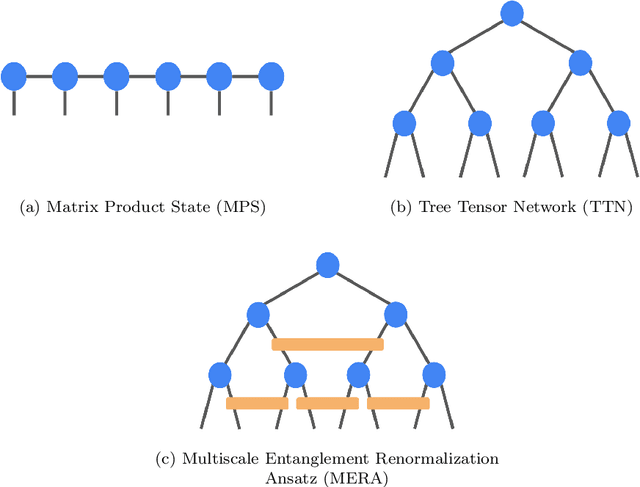
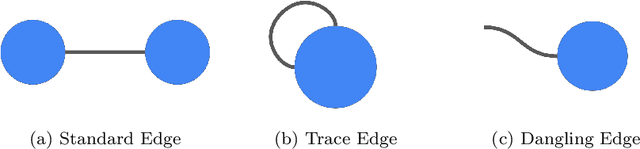
TensorNetwork is an open source library for implementing tensor network algorithms. Tensor networks are sparse data structures originally designed for simulating quantum many-body physics, but are currently also applied in a number of other research areas, including machine learning. We demonstrate the use of the API with applications both physics and machine learning, with details appearing in companion papers.