Multi-task Learning for Gaussian Graphical Regressions with High Dimensional Covariates

Gaussian graphical regression is a powerful means that regresses the precision matrix of a Gaussian graphical model on covariates, permitting the numbers of the response variables and covariates to far exceed the sample size. Model fitting is typically carried out via separate node-wise lasso regressions, ignoring the network-induced structure among these regressions. Consequently, the error rate is high, especially when the number of nodes is large. We propose a multi-task learning estimator for fitting Gaussian graphical regression models; we design a cross-task group sparsity penalty and a within task element-wise sparsity penalty, which govern the sparsity of active covariates and their effects on the graph, respectively. For computation, we consider an efficient augmented Lagrangian algorithm, which solves subproblems with a semi-smooth Newton method. For theory, we show that the error rate of the multi-task learning based estimates has much improvement over that of the separate node-wise lasso estimates, because the cross-task penalty borrows information across tasks. To address the main challenge that the tasks are entangled in a complicated correlation structure, we establish a new tail probability bound for correlated heavy-tailed (sub-exponential) variables with an arbitrary correlation structure, a useful theoretical result in its own right. Finally, the utility of our method is demonstrated through simulations as well as an application to a gene co-expression network study with brain cancer patients.

Discriminative-Generative Representation Learning for One-Class Anomaly Detection

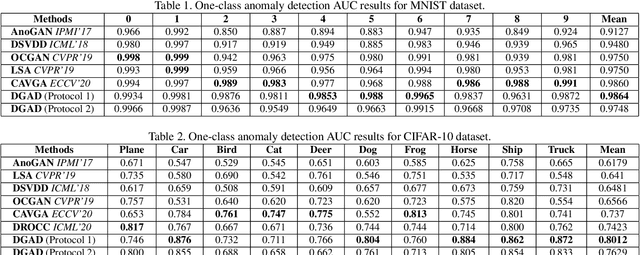
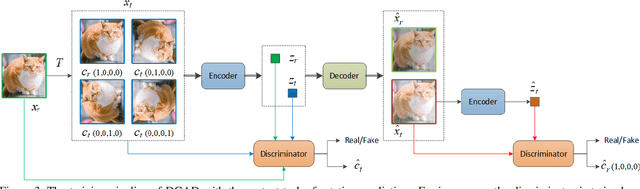
As a kind of generative self-supervised learning methods, generative adversarial nets have been widely studied in the field of anomaly detection. However, the representation learning ability of the generator is limited since it pays too much attention to pixel-level details, and generator is difficult to learn abstract semantic representations from label prediction pretext tasks as effective as discriminator. In order to improve the representation learning ability of generator, we propose a self-supervised learning framework combining generative methods and discriminative methods. The generator no longer learns representation by reconstruction error, but the guidance of discriminator, and could benefit from pretext tasks designed for discriminative methods. Our discriminative-generative representation learning method has performance close to discriminative methods and has a great advantage in speed. Our method used in one-class anomaly detection task significantly outperforms several state-of-the-arts on multiple benchmark data sets, increases the performance of the top-performing GAN-based baseline by 6% on CIFAR-10 and 2% on MVTAD.

Heterogeneous Tensor Mixture Models in High Dimensions

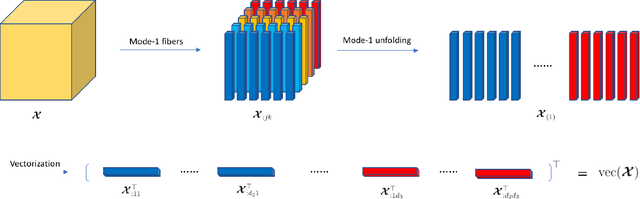
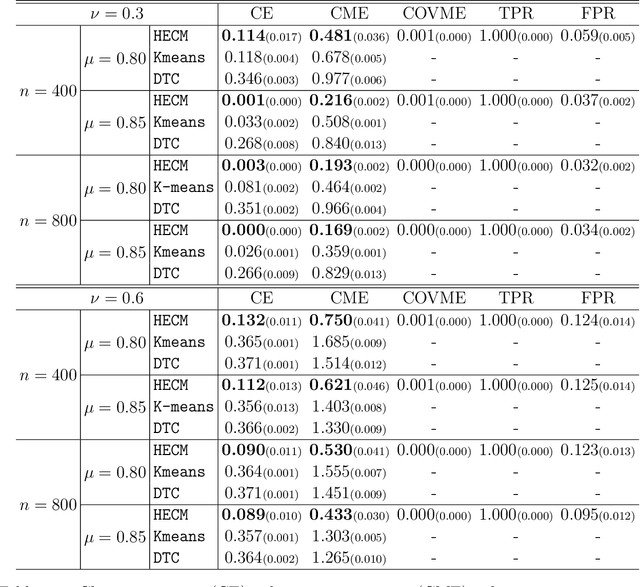
We consider the problem of jointly modeling and clustering populations of tensors by introducing a flexible high-dimensional tensor mixture model with heterogeneous covariances. The proposed mixture model exploits the intrinsic structures of tensor data, and is assumed to have means that are low-rank and internally sparse as well as heterogeneous covariances that are separable and conditionally sparse. We develop an efficient high-dimensional expectation-conditional-maximization (HECM) algorithm that breaks the challenging optimization in the M-step into several simpler conditional optimization problems, each of which is convex, admits regularization and has closed-form updating formulas. We show that the proposed HECM algorithm, with an appropriate initialization, converges geometrically to a neighborhood that is within statistical precision of the true parameter. Such a theoretical analysis is highly nontrivial due to the dual non-convexity arising from both the EM-type estimation and the non-convex objective function in the M-step. The efficacy of our proposed method is demonstrated through simulation studies and an application to an autism spectrum disorder study, where our analysis identifies important brain regions for diagnosis.

Fast Network Community Detection with Profile-Pseudo Likelihood Methods

The stochastic block model is one of the most studied network models for community detection. It is well-known that most algorithms proposed for fitting the stochastic block model likelihood function cannot scale to large-scale networks. One prominent work that overcomes this computational challenge is Amini et al.(2013), which proposed a fast pseudo-likelihood approach for fitting stochastic block models to large sparse networks. However, this approach does not have convergence guarantee, and is not well suited for small- or medium- scale networks. In this article, we propose a novel likelihood based approach that decouples row and column labels in the likelihood function, which enables a fast alternating maximization; the new method is computationally efficient, performs well for both small and large scale networks, and has provable convergence guarantee. We show that our method provides strongly consistent estimates of the communities in a stochastic block model. As demonstrated in simulation studies, the proposed method outperforms the pseudo-likelihood approach in terms of both estimation accuracy and computation efficiency, especially for large sparse networks. We further consider extensions of our proposed method to handle networks with degree heterogeneity and bipartite properties.

Latent Network Structure Learning from High Dimensional Multivariate Point Processes

Learning the latent network structure from large scale multivariate point process data is an important task in a wide range of scientific and business applications. For instance, we might wish to estimate the neuronal functional connectivity network based on spiking times recorded from a collection of neurons. To characterize the complex processes underlying the observed data, we propose a new and flexible class of nonstationary Hawkes processes that allow both excitatory and inhibitory effects. We estimate the latent network structure using an efficient sparse least squares estimation approach. Using a thinning representation, we establish concentration inequalities for the first and second order statistics of the proposed Hawkes process. Such theoretical results enable us to establish the non-asymptotic error bound and the selection consistency of the estimated parameters. Furthermore, we describe a penalized least squares based statistic for testing if the background intensity is constant in time. We demonstrate the efficacy of our proposed method through simulation studies and an application to a neuron spike train data set.

Partially Observed Dynamic Tensor Response Regression

In modern data science, dynamic tensor data is prevailing in numerous applications. An important task is to characterize the relationship between such dynamic tensor and external covariates. However, the tensor data is often only partially observed, rendering many existing methods inapplicable. In this article, we develop a regression model with partially observed dynamic tensor as the response and external covariates as the predictor. We introduce the low-rank, sparsity and fusion structures on the regression coefficient tensor, and consider a loss function projected over the observed entries. We develop an efficient non-convex alternating updating algorithm, and derive the finite-sample error bound of the actual estimator from each step of our optimization algorithm. Unobserved entries in tensor response have imposed serious challenges. As a result, our proposal differs considerably in terms of estimation algorithm, regularity conditions, as well as theoretical properties, compared to the existing tensor completion or tensor response regression solutions. We illustrate the efficacy of our proposed method using simulations, and two real applications, a neuroimaging dementia study and a digital advertising study.

Sparse Tensor Additive Regression

Tensors are becoming prevalent in modern applications such as medical imaging and digital marketing. In this paper, we propose a sparse tensor additive regression (STAR) that models a scalar response as a flexible nonparametric function of tensor covariates. The proposed model effectively exploits the sparse and low-rank structures in the tensor additive regression. We formulate the parameter estimation as a non-convex optimization problem, and propose an efficient penalized alternating minimization algorithm. We establish a non-asymptotic error bound for the estimator obtained from each iteration of the proposed algorithm, which reveals an interplay between the optimization error and the statistical rate of convergence. We demonstrate the efficacy of STAR through extensive comparative simulation studies, and an application to the click-through-rate prediction in online advertising.