Heterogeneous Tensor Mixture Models in High Dimensions

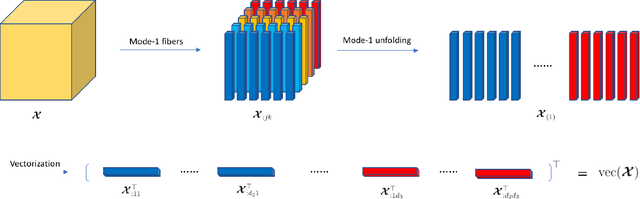
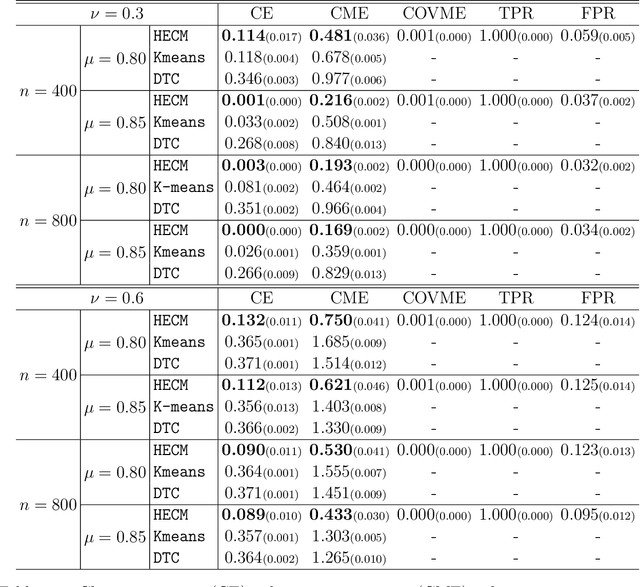
We consider the problem of jointly modeling and clustering populations of tensors by introducing a flexible high-dimensional tensor mixture model with heterogeneous covariances. The proposed mixture model exploits the intrinsic structures of tensor data, and is assumed to have means that are low-rank and internally sparse as well as heterogeneous covariances that are separable and conditionally sparse. We develop an efficient high-dimensional expectation-conditional-maximization (HECM) algorithm that breaks the challenging optimization in the M-step into several simpler conditional optimization problems, each of which is convex, admits regularization and has closed-form updating formulas. We show that the proposed HECM algorithm, with an appropriate initialization, converges geometrically to a neighborhood that is within statistical precision of the true parameter. Such a theoretical analysis is highly nontrivial due to the dual non-convexity arising from both the EM-type estimation and the non-convex objective function in the M-step. The efficacy of our proposed method is demonstrated through simulation studies and an application to an autism spectrum disorder study, where our analysis identifies important brain regions for diagnosis.

Distance Correlation Based Brain Functional Connectivity Estimation and Non-Convex Multi-Task Learning for Developmental fMRI Studies

Resting-state functional magnetic resonance imaging (rs-fMRI)-derived functional connectivity patterns have been extensively utilized to delineate global functional organization of the human brain in health, development, and neuropsychiatric disorders. In this paper, we investigate how functional connectivity in males and females differs in an age prediction framework. We first estimate functional connectivity between regions-of-interest (ROIs) using distance correlation instead of Pearson's correlation. Distance correlation, as a multivariate statistical method, explores spatial relations of voxel-wise time courses within individual ROIs and measures both linear and nonlinear dependence, capturing more complex information of between-ROI interactions. Then, a novel non-convex multi-task learning (NC-MTL) model is proposed to study age-related gender differences in functional connectivity, where age prediction for each gender group is viewed as one task. Specifically, in the proposed NC-MTL model, we introduce a composite regularizer with a combination of non-convex $\ell_{2,1-2}$ and $\ell_{1-2}$ regularization terms for selecting both common and task-specific features. Finally, we validate the proposed NC-MTL model along with distance correlation based functional connectivity on rs-fMRI of the Philadelphia Neurodevelopmental Cohort for predicting ages of both genders. The experimental results demonstrate that the proposed NC-MTL model outperforms other competing MTL models in age prediction, as well as characterizing developmental gender differences in functional connectivity patterns.

Causal inference of brain connectivity from fMRI with $ψ$-Learning Incorporated Linear non-Gaussian Acyclic Model ($ψ$-LiNGAM)

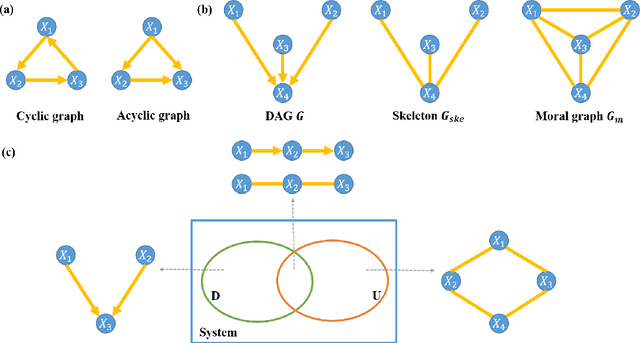
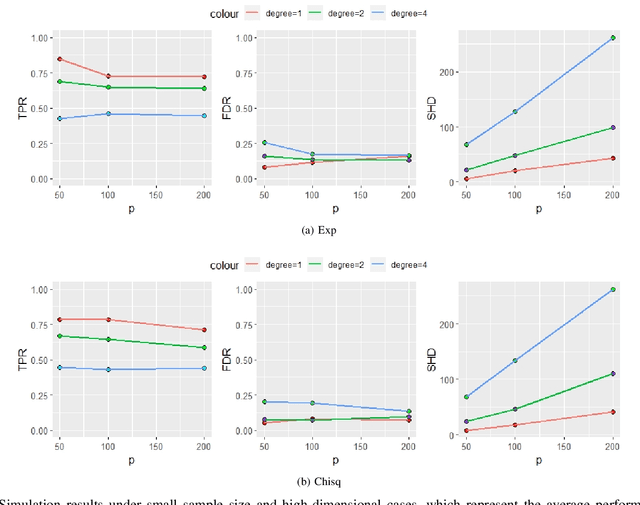
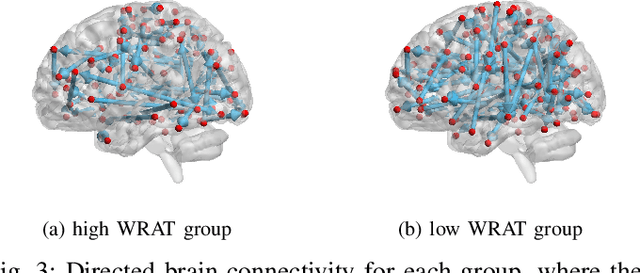
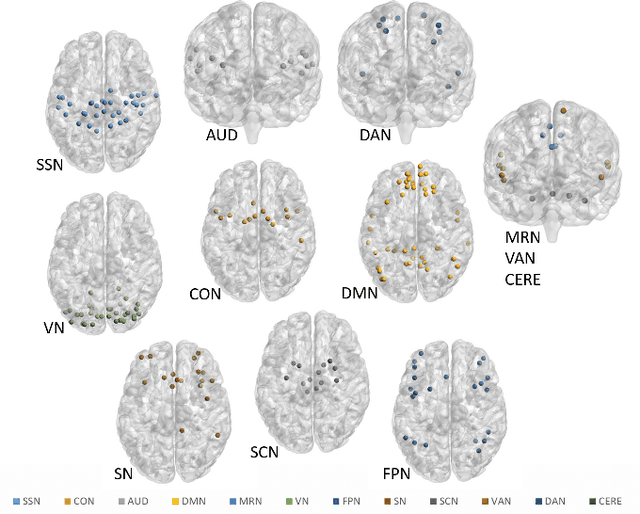
Functional connectivity (FC) has become a primary means of understanding brain functions by identifying brain network interactions and, ultimately, how those interactions produce cognitions. A popular definition of FC is by statistical associations between measured brain regions. However, this could be problematic since the associations can only provide spatial connections but not causal interactions among regions of interests. Hence, it is necessary to study their causal relationship. Directed acyclic graph (DAG) models have been applied in recent FC studies but often encountered problems such as limited sample sizes and large number of variables (namely high-dimensional problems), which lead to both computational difficulty and convergence issues. As a result, the use of DAG models is problematic, where the identification of DAG models in general is nondeterministic polynomial time hard (NP-hard). To this end, we propose a $\psi$-learning incorporated linear non-Gaussian acyclic model ($\psi$-LiNGAM). We use the association model ($\psi$-learning) to facilitate causal inferences and the model works well especially for high-dimensional cases. Our simulation results demonstrate that the proposed method is more robust and accurate than several existing ones in detecting graph structure and direction. We then applied it to the resting state fMRI (rsfMRI) data obtained from the publicly available Philadelphia Neurodevelopmental Cohort (PNC) to study the cognitive variance, which includes 855 individuals aged 8-22 years. Therein, we have identified three types of hub structure: the in-hub, out-hub and sum-hub, which correspond to the centers of receiving, sending and relaying information, respectively. We also detected 16 most important pairs of causal flows. Several of the results have been verified to be biologically significant.

A Bayesian incorporated linear non-Gaussian acyclic model for multiple directed graph estimation to study brain emotion circuit development in adolescence

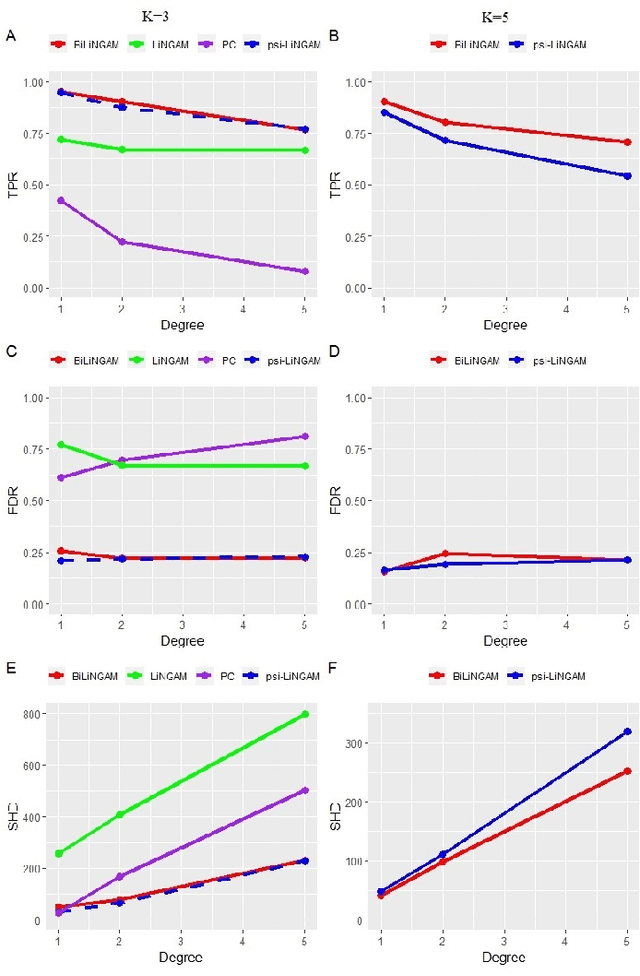
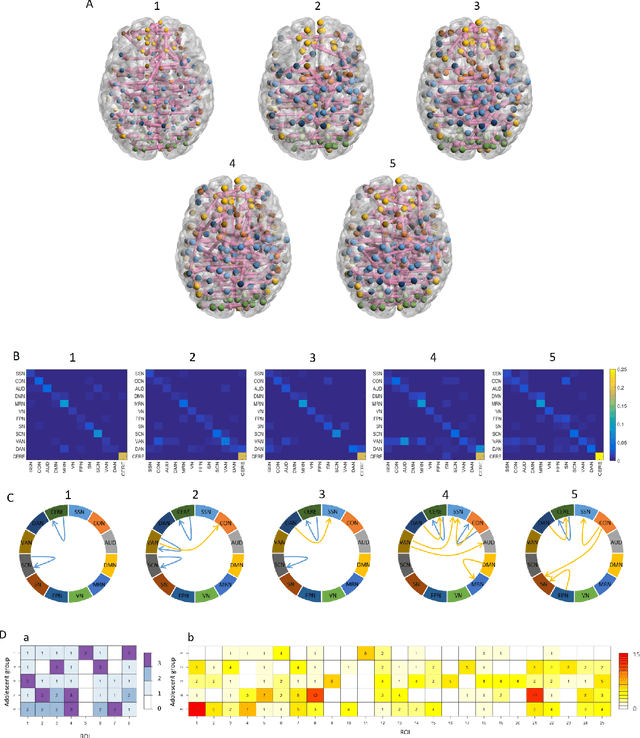
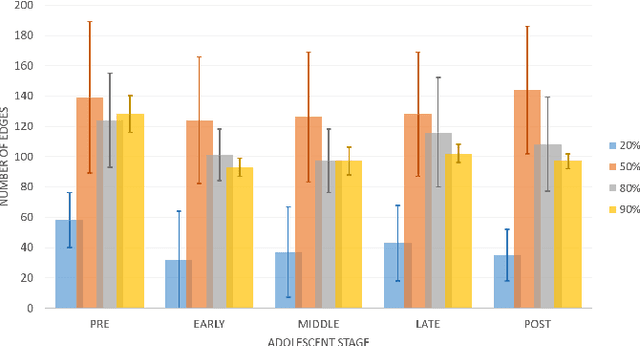
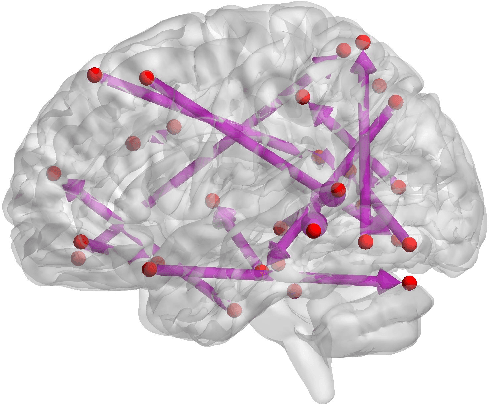
Emotion perception is essential to affective and cognitive development which involves distributed brain circuits. The ability of emotion identification begins in infancy and continues to develop throughout childhood and adolescence. Understanding the development of brain's emotion circuitry may help us explain the emotional changes observed during adolescence. Our previous study delineated the trajectory of brain functional connectivity (FC) from late childhood to early adulthood during emotion identification tasks. In this work, we endeavour to deepen our understanding from association to causation. We proposed a Bayesian incorporated linear non-Gaussian acyclic model (BiLiNGAM), which incorporated our previous association model into the prior estimation pipeline. In particular, it can jointly estimate multiple directed acyclic graphs (DAGs) for multiple age groups at different developmental stages. Simulation results indicated more stable and accurate performance over various settings, especially when the sample size was small (high-dimensional cases). We then applied to the analysis of real data from the Philadelphia Neurodevelopmental Cohort (PNC). This included 855 individuals aged 8-22 years who were divided into five different adolescent stages. Our network analysis revealed the development of emotion-related intra- and inter- modular connectivity and pinpointed several emotion-related hubs. We further categorized the hubs into two types: in-hubs and out-hubs, as the center of receiving and distributing information. Several unique developmental hub structures and group-specific patterns were also discovered. Our findings help provide a causal understanding of emotion development in the human brain.

Interpretable multimodal fusion networks reveal mechanisms of brain cognition

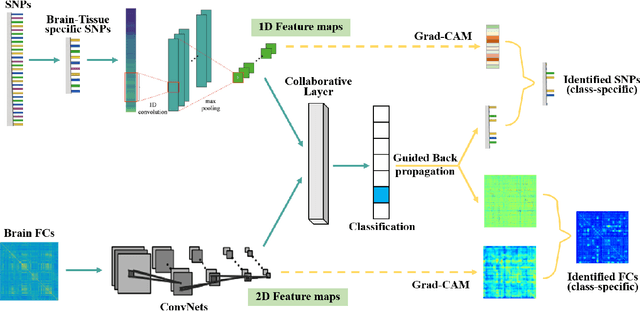
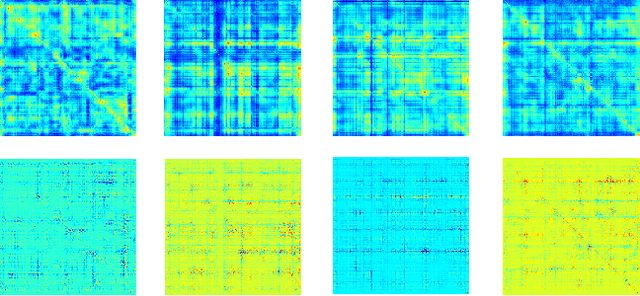
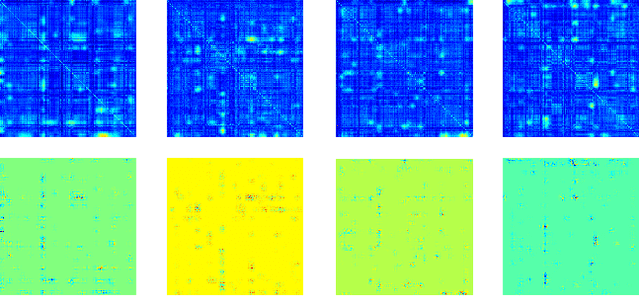
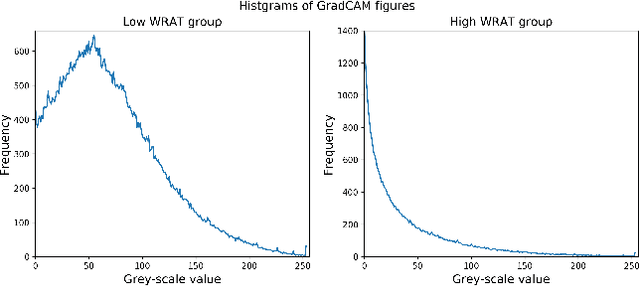
Multimodal fusion benefits disease diagnosis by providing a more comprehensive perspective. Developing algorithms is challenging due to data heterogeneity and the complex within- and between-modality associations. Deep-network-based data-fusion models have been developed to capture the complex associations and the performance in diagnosis has been improved accordingly. Moving beyond diagnosis prediction, evaluation of disease mechanisms is critically important for biomedical research. Deep-network-based data-fusion models, however, are difficult to interpret, bringing about difficulties for studying biological mechanisms. In this work, we develop an interpretable multimodal fusion model, namely gCAM-CCL, which can perform automated diagnosis and result interpretation simultaneously. The gCAM-CCL model can generate interpretable activation maps, which quantify pixel-level contributions of the input features. This is achieved by combining intermediate feature maps using gradient-based weights. Moreover, the estimated activation maps are class-specific, and the captured cross-data associations are interest/label related, which further facilitates class-specific analysis and biological mechanism analysis. We validate the gCAM-CCL model on a brain imaging-genetic study, and show gCAM-CCL's performed well for both classification and mechanism analysis. Mechanism analysis suggests that during task-fMRI scans, several object recognition related regions of interests (ROIs) are first activated and then several downstream encoding ROIs get involved. Results also suggest that the higher cognition performing group may have stronger neurotransmission signaling while the lower cognition performing group may have problem in brain/neuron development, resulting from genetic variations.

Latent Network Structure Learning from High Dimensional Multivariate Point Processes

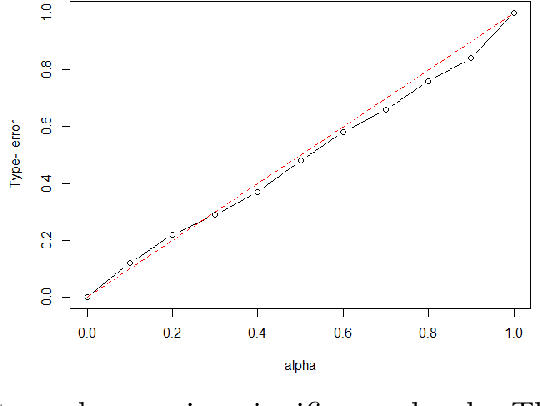
Learning the latent network structure from large scale multivariate point process data is an important task in a wide range of scientific and business applications. For instance, we might wish to estimate the neuronal functional connectivity network based on spiking times recorded from a collection of neurons. To characterize the complex processes underlying the observed data, we propose a new and flexible class of nonstationary Hawkes processes that allow both excitatory and inhibitory effects. We estimate the latent network structure using an efficient sparse least squares estimation approach. Using a thinning representation, we establish concentration inequalities for the first and second order statistics of the proposed Hawkes process. Such theoretical results enable us to establish the non-asymptotic error bound and the selection consistency of the estimated parameters. Furthermore, we describe a penalized least squares based statistic for testing if the background intensity is constant in time. We demonstrate the efficacy of our proposed method through simulation studies and an application to a neuron spike train data set.