Heterogeneous Tensor Mixture Models in High Dimensions
Paper and Code
Apr 15, 2021
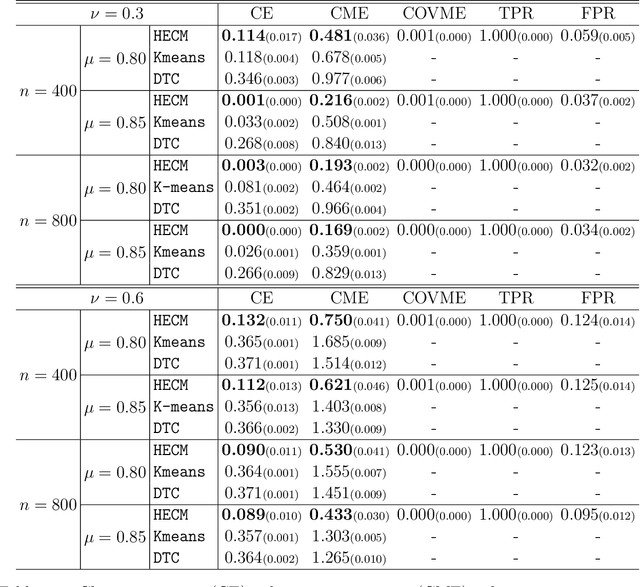


We consider the problem of jointly modeling and clustering populations of tensors by introducing a flexible high-dimensional tensor mixture model with heterogeneous covariances. The proposed mixture model exploits the intrinsic structures of tensor data, and is assumed to have means that are low-rank and internally sparse as well as heterogeneous covariances that are separable and conditionally sparse. We develop an efficient high-dimensional expectation-conditional-maximization (HECM) algorithm that breaks the challenging optimization in the M-step into several simpler conditional optimization problems, each of which is convex, admits regularization and has closed-form updating formulas. We show that the proposed HECM algorithm, with an appropriate initialization, converges geometrically to a neighborhood that is within statistical precision of the true parameter. Such a theoretical analysis is highly nontrivial due to the dual non-convexity arising from both the EM-type estimation and the non-convex objective function in the M-step. The efficacy of our proposed method is demonstrated through simulation studies and an application to an autism spectrum disorder study, where our analysis identifies important brain regions for diagnosis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge