DiffIM: Differentiable Influence Minimization with Surrogate Modeling and Continuous Relaxation

In social networks, people influence each other through social links, which can be represented as propagation among nodes in graphs. Influence minimization (IMIN) is the problem of manipulating the structures of an input graph (e.g., removing edges) to reduce the propagation among nodes. IMIN can represent time-critical real-world applications, such as rumor blocking, but IMIN is theoretically difficult and computationally expensive. Moreover, the discrete nature of IMIN hinders the usage of powerful machine learning techniques, which requires differentiable computation. In this work, we propose DiffIM, a novel method for IMIN with two differentiable schemes for acceleration: (1) surrogate modeling for efficient influence estimation, which avoids time-consuming simulations (e.g., Monte Carlo), and (2) the continuous relaxation of decisions, which avoids the evaluation of individual discrete decisions (e.g., removing an edge). We further propose a third accelerating scheme, gradient-driven selection, that chooses edges instantly based on gradients without optimization (spec., gradient descent iterations) on each test instance. Through extensive experiments on real-world graphs, we show that each proposed scheme significantly improves speed with little (or even no) IMIN performance degradation. Our method is Pareto-optimal (i.e., no baseline is faster and more effective than it) and typically several orders of magnitude (spec., up to 15,160X) faster than the most effective baseline while being more effective.

TensorCodec: Compact Lossy Compression of Tensors without Strong Data Assumptions

Many real-world datasets are represented as tensors, i.e., multi-dimensional arrays of numerical values. Storing them without compression often requires substantial space, which grows exponentially with the order. While many tensor compression algorithms are available, many of them rely on strong data assumptions regarding its order, sparsity, rank, and smoothness. In this work, we propose TENSORCODEC, a lossy compression algorithm for general tensors that do not necessarily adhere to strong input data assumptions. TENSORCODEC incorporates three key ideas. The first idea is Neural Tensor-Train Decomposition (NTTD) where we integrate a recurrent neural network into Tensor-Train Decomposition to enhance its expressive power and alleviate the limitations imposed by the low-rank assumption. Another idea is to fold the input tensor into a higher-order tensor to reduce the space required by NTTD. Finally, the mode indices of the input tensor are reordered to reveal patterns that can be exploited by NTTD for improved approximation. Our analysis and experiments on 8 real-world datasets demonstrate that TENSORCODEC is (a) Concise: it gives up to 7.38x more compact compression than the best competitor with similar reconstruction error, (b) Accurate: given the same budget for compressed size, it yields up to 3.33x more accurate reconstruction than the best competitor, (c) Scalable: its empirical compression time is linear in the number of tensor entries, and it reconstructs each entry in logarithmic time. Our code and datasets are available at https://github.com/kbrother/TensorCodec.

NeuKron: Constant-Size Lossy Compression of Sparse Reorderable Matrices and Tensors

Many real-world data are naturally represented as a sparse reorderable matrix, whose rows and columns can be arbitrarily ordered (e.g., the adjacency matrix of a bipartite graph). Storing a sparse matrix in conventional ways requires an amount of space linear in the number of non-zeros, and lossy compression of sparse matrices (e.g., Truncated SVD) typically requires an amount of space linear in the number of rows and columns. In this work, we propose NeuKron for compressing a sparse reorderable matrix into a constant-size space. NeuKron generalizes Kronecker products using a recurrent neural network with a constant number of parameters. NeuKron updates the parameters so that a given matrix is approximated by the product and reorders the rows and columns of the matrix to facilitate the approximation. The updates take time linear in the number of non-zeros in the input matrix, and the approximation of each entry can be retrieved in logarithmic time. We also extend NeuKron to compress sparse reorderable tensors (e.g. multi-layer graphs), which generalize matrices. Through experiments on ten real-world datasets, we show that NeuKron is (a) Compact: requiring up to five orders of magnitude less space than its best competitor with similar approximation errors, (b) Accurate: giving up to 10x smaller approximation error than its best competitors with similar size outputs, and (c) Scalable: successfully compressing a matrix with over 230 million non-zero entries.

BeGin: Extensive Benchmark Scenarios and An Easy-to-use Framework for Graph Continual Learning

Continual Learning (CL) is the process of learning ceaselessly a sequence of tasks. Most existing CL methods deal with independent data (e.g., images and text) for which many benchmark frameworks and results under standard experimental settings are available. CL methods for graph data, however, are surprisingly underexplored because of (a) the lack of standard experimental settings, especially regarding how to deal with the dependency between instances, (b) the lack of benchmark datasets and scenarios, and (c) high complexity in implementation and evaluation due to the dependency. In this paper, regarding (a), we define four standard incremental settings (task-, class-, domain-, and time-incremental settings) for graph data, which are naturally applied to many node-, link-, and graph-level problems. Regarding (b), we provide 23 benchmark scenarios based on 14 real-world graphs. Regarding (c), we develop BeGin, an easy and fool-proof framework for graph CL. BeGin is easily extended since it is modularized with reusable modules for data processing, algorithm design, and evaluation. Especially, the evaluation module is completely separated from user code to eliminate potential mistakes in evaluation. Using all above, we report extensive benchmark results of seven graph CL methods. Compared to the latest benchmark for graph CL, using BeGin, we cover three times more combinations of incremental settings and levels of problems.

Effective Training Strategies for Deep-learning-based Precipitation Nowcasting and Estimation

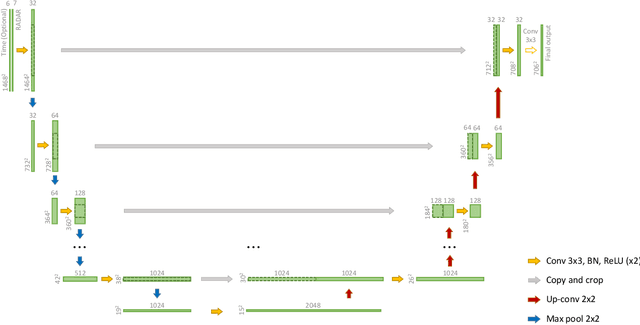
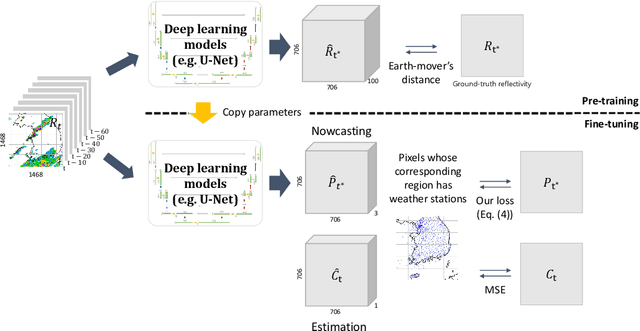
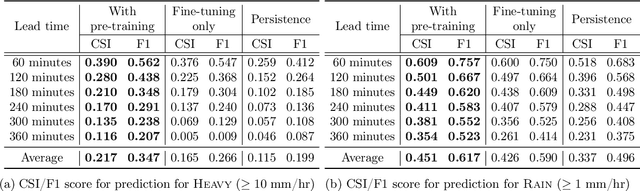
Deep learning has been successfully applied to precipitation nowcasting. In this work, we propose a pre-training scheme and a new loss function for improving deep-learning-based nowcasting. First, we adapt U-Net, a widely-used deep-learning model, for the two problems of interest here: precipitation nowcasting and precipitation estimation from radar images. We formulate the former as a classification problem with three precipitation intervals and the latter as a regression problem. For these tasks, we propose to pre-train the model to predict radar images in the near future without requiring ground-truth precipitation, and we also propose the use of a new loss function for fine-tuning to mitigate the class imbalance problem. We demonstrate the effectiveness of our approach using radar images and precipitation datasets collected from South Korea over seven years. It is highlighted that our pre-training scheme and new loss function improve the critical success index (CSI) of nowcasting of heavy rainfall (at least 10 mm/hr) by up to 95.7% and 43.6%, respectively, at a 5-hr lead time. We also demonstrate that our approach reduces the precipitation estimation error by up to 10.7%, compared to the conventional approach, for light rainfall (between 1 and 10 mm/hr). Lastly, we report the sensitivity of our approach to different resolutions and a detailed analysis of four cases of heavy rainfall.

Learning to Pool in Graph Neural Networks for Extrapolation

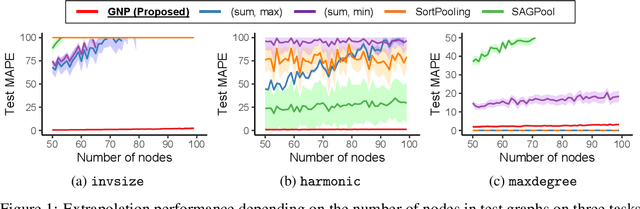
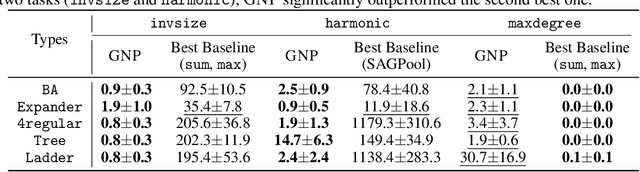
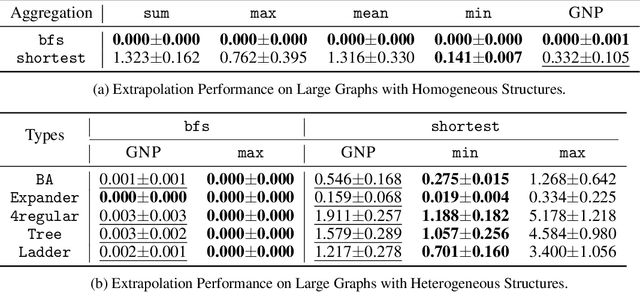
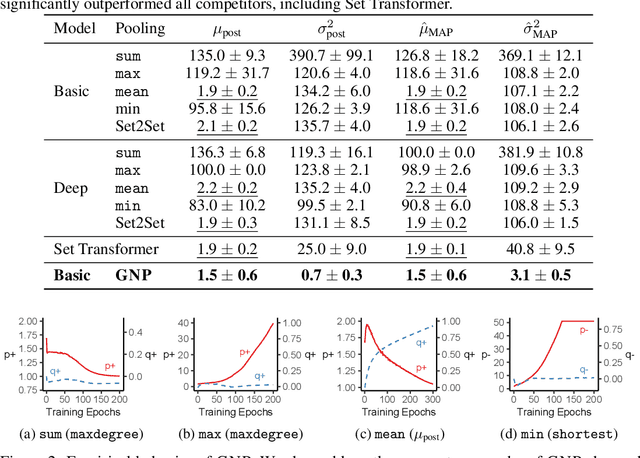
Graph neural networks (GNNs) are one of the most popular approaches to using deep learning on graph-structured data, and they have shown state-of-the-art performances on a variety of tasks. However, according to a recent study, a careful choice of pooling functions, which are used for the aggregation or readout operation in GNNs, is crucial for enabling GNNs to extrapolate. Without the ideal combination of pooling functions, which varies across tasks, GNNs completely fail to generalize to out-of-distribution data, while the number of possible combinations grows exponentially with the number of layers. In this paper, we present GNP, a $L^p$ norm-like pooling function that is trainable end-to-end for any given task. Notably, GNP generalizes most of the widely-used pooling functions. We verify experimentally that simply replacing all pooling functions with GNP enables GNNs to extrapolate well on many node-level, graph-level, and set-related tasks; and GNP sometimes performs even better than optimal combinations of existing pooling functions.

MONSTOR: An Inductive Approach for Estimating and Maximizing Influence over Unseen Social Networks

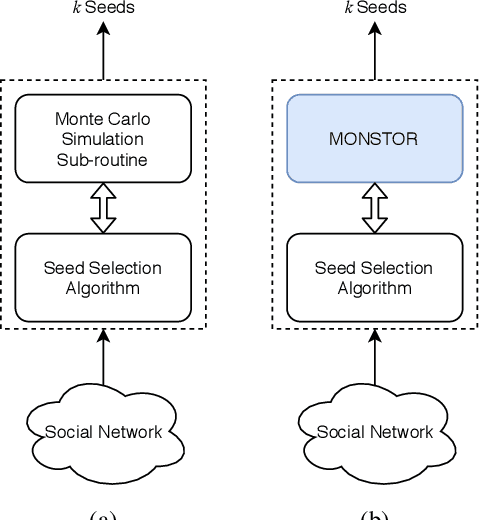
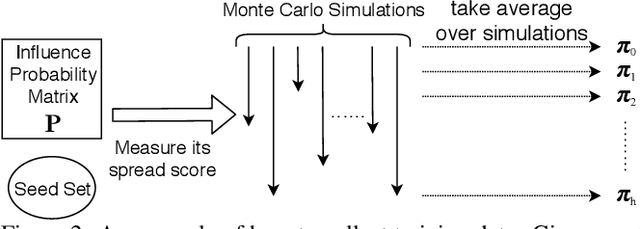
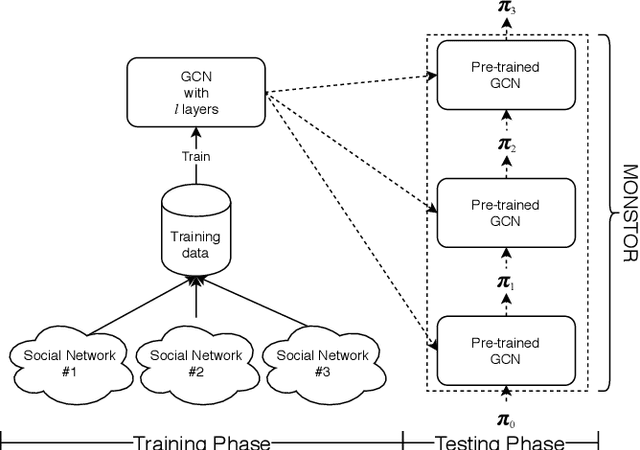
Influence maximization (IM) is one of the most important problems in social network analysis. Its objective is to find a given number of seed nodes who maximize the spread of information through a social network. Since it is an NP-hard problem, many approximate/heuristic methods have been developed, and a number of them repeats Monte Carlo (MC) simulations over and over, specifically tens of thousands of times or more per potential seed set, to reliably estimate the influence. In this work, we present an inductive machine learning method, called Monte Carlo Simulator (MONSTOR), to predict the results of MC simulations on networks unseen during training. MONSTOR can greatly accelerate existing IM methods by replacing repeated MC simulations. In our experiments, MONSTOR achieves near-perfect accuracy on unseen real social networks with little sacrifice of accuracy in IM use cases.