Learning to Pool in Graph Neural Networks for Extrapolation
Paper and Code
Jun 11, 2021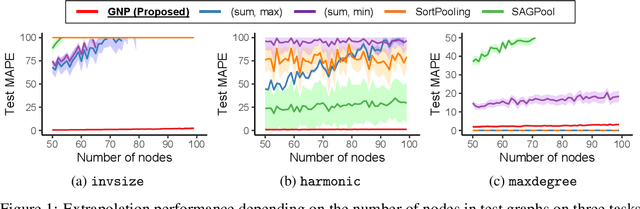
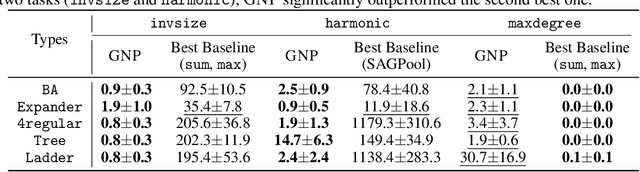
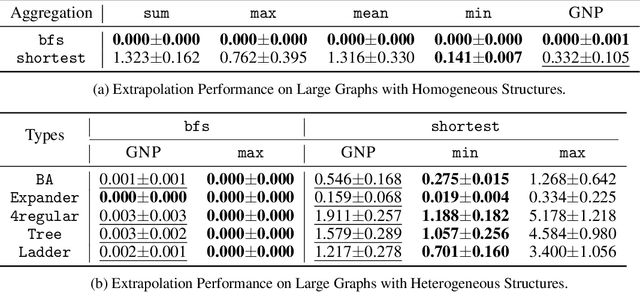
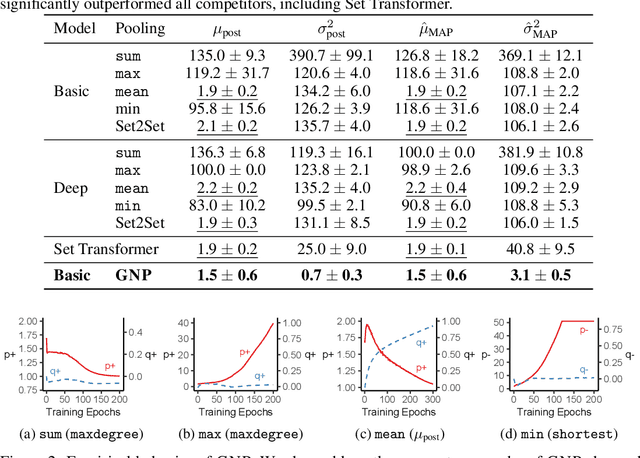
Graph neural networks (GNNs) are one of the most popular approaches to using deep learning on graph-structured data, and they have shown state-of-the-art performances on a variety of tasks. However, according to a recent study, a careful choice of pooling functions, which are used for the aggregation or readout operation in GNNs, is crucial for enabling GNNs to extrapolate. Without the ideal combination of pooling functions, which varies across tasks, GNNs completely fail to generalize to out-of-distribution data, while the number of possible combinations grows exponentially with the number of layers. In this paper, we present GNP, a $L^p$ norm-like pooling function that is trainable end-to-end for any given task. Notably, GNP generalizes most of the widely-used pooling functions. We verify experimentally that simply replacing all pooling functions with GNP enables GNNs to extrapolate well on many node-level, graph-level, and set-related tasks; and GNP sometimes performs even better than optimal combinations of existing pooling functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge