Simple yet Effective Node Property Prediction on Edge Streams under Distribution Shifts

The problem of predicting node properties (e.g., node classes) in graphs has received significant attention due to its broad range of applications. Graphs from real-world datasets often evolve over time, with newly emerging edges and dynamically changing node properties, posing a significant challenge for this problem. In response, temporal graph neural networks (TGNNs) have been developed to predict dynamic node properties from a stream of emerging edges. However, our analysis reveals that most TGNN-based methods are (a) far less effective without proper node features and, due to their complex model architectures, (b) vulnerable to distribution shifts. In this paper, we propose SPLASH, a simple yet powerful method for predicting node properties on edge streams under distribution shifts. Our key contributions are as follows: (1) we propose feature augmentation methods and an automatic feature selection method for edge streams, which improve the effectiveness of TGNNs, (2) we propose a lightweight MLP-based TGNN architecture that is highly efficient and robust under distribution shifts, and (3) we conduct extensive experiments to evaluate the accuracy, efficiency, generalization, and qualitative performance of the proposed method and its competitors on dynamic node classification, dynamic anomaly detection, and node affinity prediction tasks across seven real-world datasets.

TensorCodec: Compact Lossy Compression of Tensors without Strong Data Assumptions

Many real-world datasets are represented as tensors, i.e., multi-dimensional arrays of numerical values. Storing them without compression often requires substantial space, which grows exponentially with the order. While many tensor compression algorithms are available, many of them rely on strong data assumptions regarding its order, sparsity, rank, and smoothness. In this work, we propose TENSORCODEC, a lossy compression algorithm for general tensors that do not necessarily adhere to strong input data assumptions. TENSORCODEC incorporates three key ideas. The first idea is Neural Tensor-Train Decomposition (NTTD) where we integrate a recurrent neural network into Tensor-Train Decomposition to enhance its expressive power and alleviate the limitations imposed by the low-rank assumption. Another idea is to fold the input tensor into a higher-order tensor to reduce the space required by NTTD. Finally, the mode indices of the input tensor are reordered to reveal patterns that can be exploited by NTTD for improved approximation. Our analysis and experiments on 8 real-world datasets demonstrate that TENSORCODEC is (a) Concise: it gives up to 7.38x more compact compression than the best competitor with similar reconstruction error, (b) Accurate: given the same budget for compressed size, it yields up to 3.33x more accurate reconstruction than the best competitor, (c) Scalable: its empirical compression time is linear in the number of tensor entries, and it reconstructs each entry in logarithmic time. Our code and datasets are available at https://github.com/kbrother/TensorCodec.

NeuKron: Constant-Size Lossy Compression of Sparse Reorderable Matrices and Tensors

Many real-world data are naturally represented as a sparse reorderable matrix, whose rows and columns can be arbitrarily ordered (e.g., the adjacency matrix of a bipartite graph). Storing a sparse matrix in conventional ways requires an amount of space linear in the number of non-zeros, and lossy compression of sparse matrices (e.g., Truncated SVD) typically requires an amount of space linear in the number of rows and columns. In this work, we propose NeuKron for compressing a sparse reorderable matrix into a constant-size space. NeuKron generalizes Kronecker products using a recurrent neural network with a constant number of parameters. NeuKron updates the parameters so that a given matrix is approximated by the product and reorders the rows and columns of the matrix to facilitate the approximation. The updates take time linear in the number of non-zeros in the input matrix, and the approximation of each entry can be retrieved in logarithmic time. We also extend NeuKron to compress sparse reorderable tensors (e.g. multi-layer graphs), which generalize matrices. Through experiments on ten real-world datasets, we show that NeuKron is (a) Compact: requiring up to five orders of magnitude less space than its best competitor with similar approximation errors, (b) Accurate: giving up to 10x smaller approximation error than its best competitors with similar size outputs, and (c) Scalable: successfully compressing a matrix with over 230 million non-zero entries.

Learning to Pool in Graph Neural Networks for Extrapolation

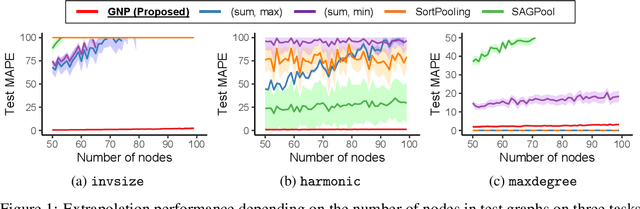
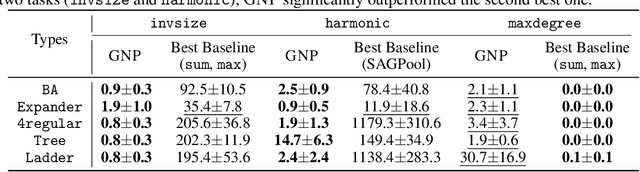
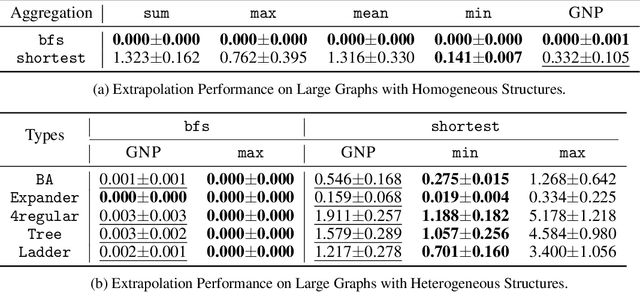
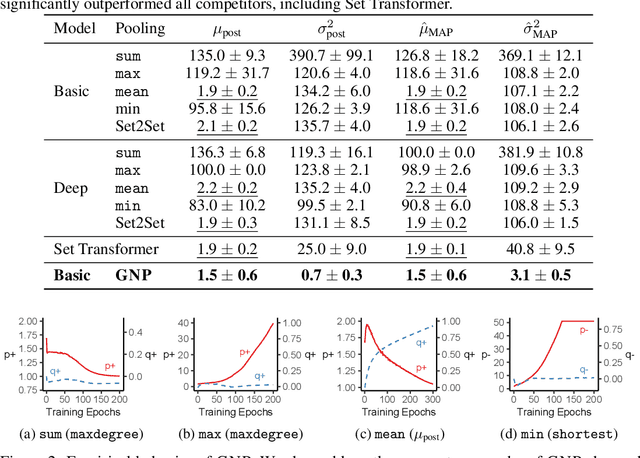
Graph neural networks (GNNs) are one of the most popular approaches to using deep learning on graph-structured data, and they have shown state-of-the-art performances on a variety of tasks. However, according to a recent study, a careful choice of pooling functions, which are used for the aggregation or readout operation in GNNs, is crucial for enabling GNNs to extrapolate. Without the ideal combination of pooling functions, which varies across tasks, GNNs completely fail to generalize to out-of-distribution data, while the number of possible combinations grows exponentially with the number of layers. In this paper, we present GNP, a $L^p$ norm-like pooling function that is trainable end-to-end for any given task. Notably, GNP generalizes most of the widely-used pooling functions. We verify experimentally that simply replacing all pooling functions with GNP enables GNNs to extrapolate well on many node-level, graph-level, and set-related tasks; and GNP sometimes performs even better than optimal combinations of existing pooling functions.

SliceNStitch: Continuous CP Decomposition of Sparse Tensor Streams

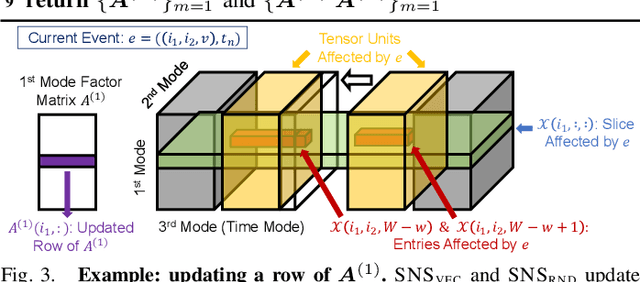
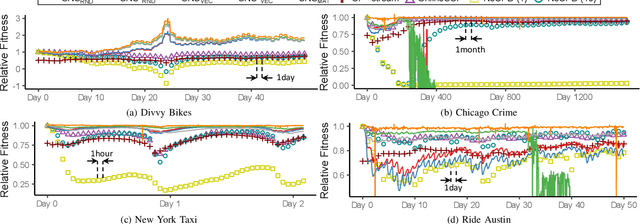
Consider traffic data (i.e., triplets in the form of source-destination-timestamp) that grow over time. Tensors (i.e., multi-dimensional arrays) with a time mode are widely used for modeling and analyzing such multi-aspect data streams. In such tensors, however, new entries are added only once per period, which is often an hour, a day, or even a year. This discreteness of tensors has limited their usage for real-time applications, where new data should be analyzed instantly as it arrives. How can we analyze time-evolving multi-aspect sparse data 'continuously' using tensors where time is'discrete'? We propose SLICENSTITCH for continuous CANDECOMP/PARAFAC (CP) decomposition, which has numerous time-critical applications, including anomaly detection, recommender systems, and stock market prediction. SLICENSTITCH changes the starting point of each period adaptively, based on the current time, and updates factor matrices (i.e., outputs of CP decomposition) instantly as new data arrives. We show, theoretically and experimentally, that SLICENSTITCH is (1) 'Any time': updating factor matrices immediately without having to wait until the current time period ends, (2) Fast: with constant-time updates up to 464x faster than online methods, and (3) Accurate: with fitness comparable (specifically, 72 ~ 100%) to offline methods.