Jieun Choi
Department of Physics, Hanyang University
FireQ: Fast INT4-FP8 Kernel and RoPE-aware Quantization for LLM Inference Acceleration
May 28, 2025Abstract:As large language models become increasingly prevalent, memory bandwidth constraints significantly limit inference throughput, motivating post-training quantization (PTQ). In this paper, we propose FireQ, a co-designed PTQ framework and an INT4-FP8 matrix multiplication kernel that accelerates LLM inference across all linear layers. Specifically, FireQ quantizes linear layer weights and key-values to INT4, and activations and queries to FP8, significantly enhancing throughput. Additionally, we introduce a three-stage pipelining for the prefill phase, which modifies the FlashAttention-3 kernel, effectively reducing time-to-first-token in the prefill phase. To minimize accuracy loss from quantization, we develop novel outlier smoothing techniques tailored separately for linear and attention layers. In linear layers, we explicitly use per-tensor scaling to prevent underflow caused by the FP8 quantization scaling factor of INT4 quantization, and channel-wise scaling to compensate for coarse granularity of INT4. In attention layers, we address quantization challenges posed by rotary positional embeddings (RoPE) by combining pre-RoPE and post-RoPE scaling strategies. FireQ significantly outperforms state-of-the-art methods, achieving 1.68x faster inference in feed-forward network layers on Llama2-7B and 1.26x faster prefill phase performance on Llama3-8B compared to QServe, with negligible accuracy loss.
MGHanD: Multi-modal Guidance for authentic Hand Diffusion
Mar 11, 2025

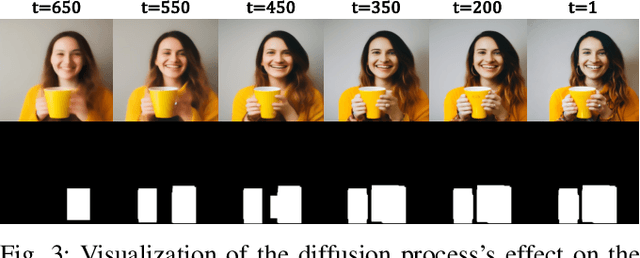

Abstract:Diffusion-based methods have achieved significant successes in T2I generation, providing realistic images from text prompts. Despite their capabilities, these models face persistent challenges in generating realistic human hands, often producing images with incorrect finger counts and structurally deformed hands. MGHanD addresses this challenge by applying multi-modal guidance during the inference process. For visual guidance, we employ a discriminator trained on a dataset comprising paired real and generated images with captions, derived from various hand-in-the-wild datasets. We also employ textual guidance with LoRA adapter, which learns the direction from `hands' towards more detailed prompts such as `natural hands', and `anatomically correct fingers' at the latent level. A cumulative hand mask which is gradually enlarged in the assigned time step is applied to the added guidance, allowing the hand to be refined while maintaining the rich generative capabilities of the pre-trained model. In the experiments, our method achieves superior hand generation qualities, without any specific conditions or priors. We carry out both quantitative and qualitative evaluations, along with user studies, to showcase the benefits of our approach in producing high-quality hand images.
A Survey on Integration of Large Language Models with Intelligent Robots
Apr 14, 2024Abstract:In recent years, the integration of large language models (LLMs) has revolutionized the field of robotics, enabling robots to communicate, understand, and reason with human-like proficiency. This paper explores the multifaceted impact of LLMs on robotics, addressing key challenges and opportunities for leveraging these models across various domains. By categorizing and analyzing LLM applications within core robotics elements -- communication, perception, planning, and control -- we aim to provide actionable insights for researchers seeking to integrate LLMs into their robotic systems. Our investigation focuses on LLMs developed post-GPT-3.5, primarily in text-based modalities while also considering multimodal approaches for perception and control. We offer comprehensive guidelines and examples for prompt engineering, facilitating beginners' access to LLM-based robotics solutions. Through tutorial-level examples and structured prompt construction, we illustrate how LLM-guided enhancements can be seamlessly integrated into robotics applications. This survey serves as a roadmap for researchers navigating the evolving landscape of LLM-driven robotics, offering a comprehensive overview and practical guidance for harnessing the power of language models in robotics development.
Review Learning: Alleviating Catastrophic Forgetting with Generative Replay without Generator
Oct 17, 2022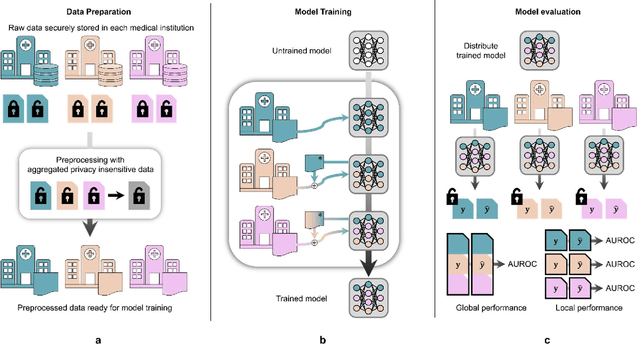

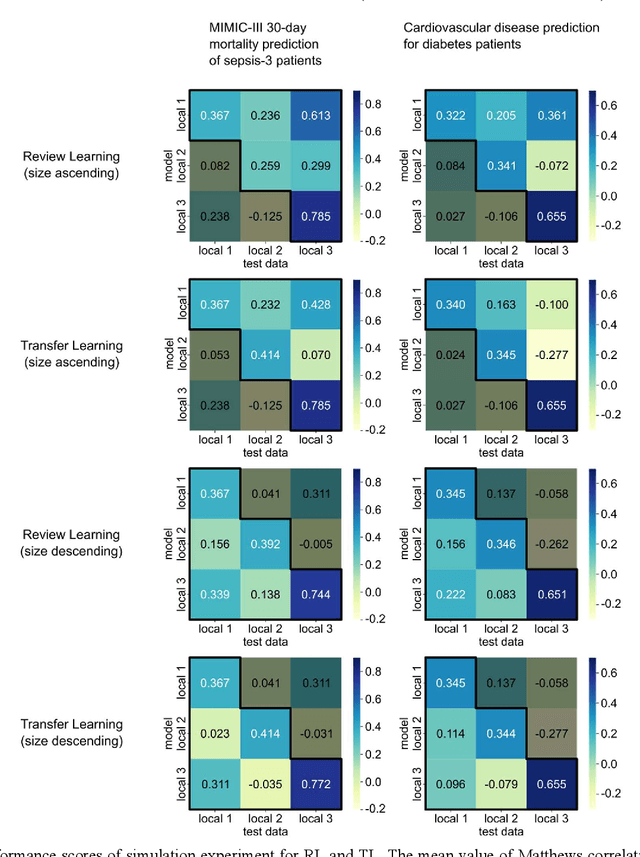
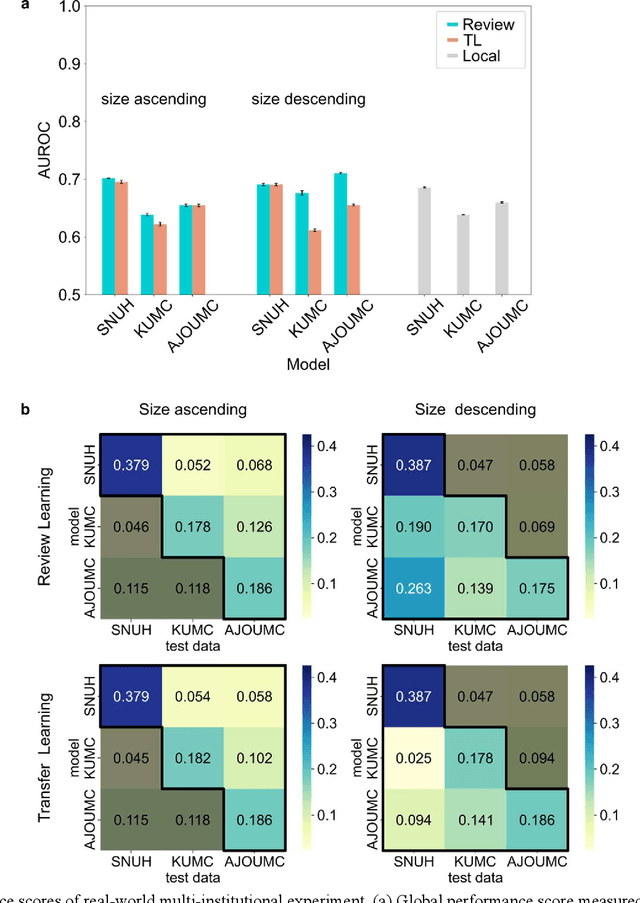
Abstract:When a deep learning model is sequentially trained on different datasets, it forgets the knowledge acquired from previous data, a phenomenon known as catastrophic forgetting. It deteriorates performance of the deep learning model on diverse datasets, which is critical in privacy-preserving deep learning (PPDL) applications based on transfer learning (TL). To overcome this, we propose review learning (RL), a generative-replay-based continual learning technique that does not require a separate generator. Data samples are generated from the memory stored within the synaptic weights of the deep learning model which are used to review knowledge acquired from previous datasets. The performance of RL was validated through PPDL experiments. Simulations and real-world medical multi-institutional experiments were conducted using three types of binary classification electronic health record data. In the real-world experiments, the global area under the receiver operating curve was 0.710 for RL and 0.655 for TL. Thus, RL was highly effective in retaining previously learned knowledge.
Learning to increase matching efficiency in identifying additional b-jets in the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ process
Mar 16, 2021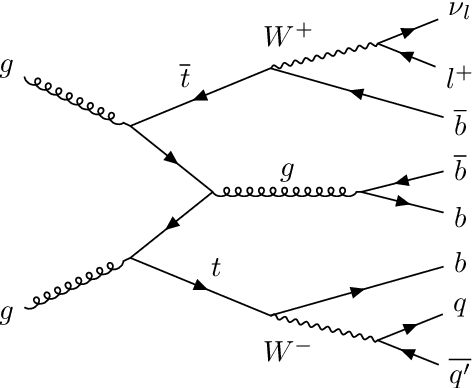
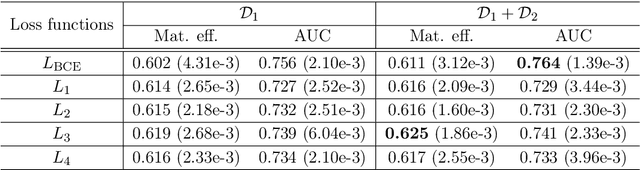
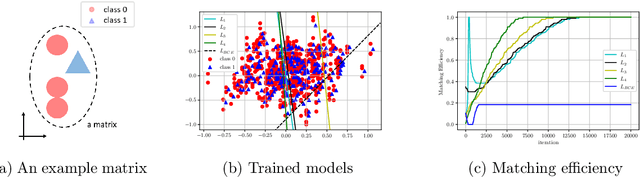
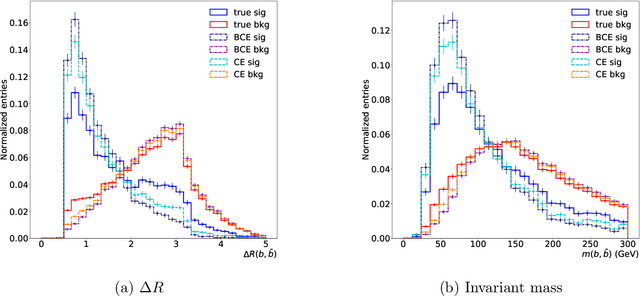
Abstract:The $\text{t}\bar{\text{t}}\text{H}(\text{b}\bar{\text{b}})$ process is an essential channel to reveal the Higgs properties but has an irreducible background from the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ process, which produces a top quark pair in association with a b quark pair. Therefore, understanding the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ process is crucial for improving the sensitivity of a search for the $\text{t}\bar{\text{t}}\text{H}(\text{b}\bar{\text{b}})$ process. To this end, when measuring the differential cross-section of the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ process, we need to distinguish the b-jets originated from top quark decays, and additional b-jets originated from gluon splitting. Since there are no simple identification rules, we adopt deep learning methods to learn from data to identify the additional b-jets from the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ events. Specifically, by exploiting the special structure of the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ event data, we propose several loss functions that can be minimized to directly increase the matching efficiency, the accuracy of identifying additional b-jets. We discuss the difference between our method and another deep learning-based approach based on binary classification arXiv:1910.14535 using synthetic data. We then verify that additional b-jets can be identified more accurately by increasing matching efficiency directly rather than the binary classification accuracy, using simulated $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ event data in the lepton+jets channel from pp collision at $\sqrt{s}$ = 13 TeV.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge