Chain-of-Programming (CoP) : Empowering Large Language Models for Geospatial Code Generation

With the rapid growth of interdisciplinary demands for geospatial modeling and the rise of large language models (LLMs), geospatial code generation technology has seen significant advancements. However, existing LLMs often face challenges in the geospatial code generation process due to incomplete or unclear user requirements and insufficient knowledge of specific platform syntax rules, leading to the generation of non-executable code, a phenomenon known as "code hallucination." To address this issue, this paper proposes a Chain of Programming (CoP) framework, which decomposes the code generation process into five steps: requirement analysis, algorithm design, code implementation, code debugging, and code annotation. The framework incorporates a shared information pool, knowledge base retrieval, and user feedback mechanisms, forming an end-to-end code generation flow from requirements to code without the need for model fine-tuning. Based on a geospatial problem classification framework and evaluation benchmarks, the CoP strategy significantly improves the logical clarity, syntactical correctness, and executability of the generated code, with improvements ranging from 3.0% to 48.8%. Comparative and ablation experiments further validate the superiority of the CoP strategy over other optimization approaches and confirm the rationality and necessity of its key components. Through case studies on building data visualization and fire data analysis, this paper demonstrates the application and effectiveness of CoP in various geospatial scenarios. The CoP framework offers a systematic, step-by-step approach to LLM-based geospatial code generation tasks, significantly enhancing code generation performance in geospatial tasks and providing valuable insights for code generation in other vertical domains.

Potential-Based Intrinsic Motivation: Preserving Optimality With Complex, Non-Markovian Shaping Rewards

Recently there has been a proliferation of intrinsic motivation (IM) reward-shaping methods to learn in complex and sparse-reward environments. These methods can often inadvertently change the set of optimal policies in an environment, leading to suboptimal behavior. Previous work on mitigating the risks of reward shaping, particularly through potential-based reward shaping (PBRS), has not been applicable to many IM methods, as they are often complex, trainable functions themselves, and therefore dependent on a wider set of variables than the traditional reward functions that PBRS was developed for. We present an extension to PBRS that we prove preserves the set of optimal policies under a more general set of functions than has been previously proven. We also present {\em Potential-Based Intrinsic Motivation} (PBIM) and {\em Generalized Reward Matching} (GRM), methods for converting IM rewards into a potential-based form that are useable without altering the set of optimal policies. Testing in the MiniGrid DoorKey and Cliff Walking environments, we demonstrate that PBIM and GRM successfully prevent the agent from converging to a suboptimal policy and can speed up training. Additionally, we prove that GRM is sufficiently general as to encompass all potential-based reward shaping functions. This paper expands on previous work introducing the PBIM method, and provides an extension to the more general method of GRM, as well as additional proofs, experimental results, and discussion.

An advanced spatio-temporal convolutional recurrent neural network for storm surge predictions

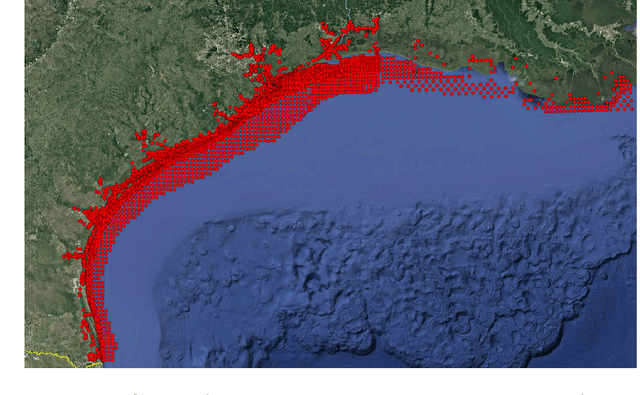
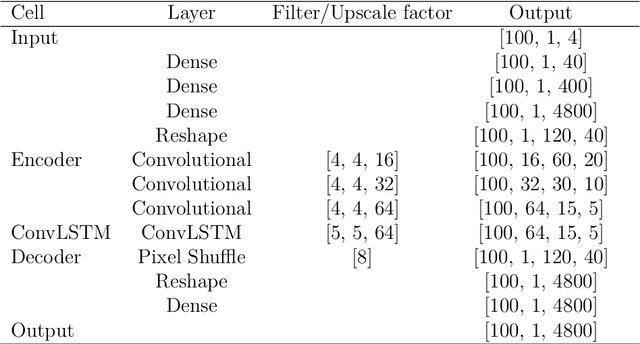
In this research paper, we study the capability of artificial neural network models to emulate storm surge based on the storm track/size/intensity history, leveraging a database of synthetic storm simulations. Traditionally, Computational Fluid Dynamics solvers are employed to numerically solve the storm surge governing equations that are Partial Differential Equations and are generally very costly to simulate. This study presents a neural network model that can predict storm surge, informed by a database of synthetic storm simulations. This model can serve as a fast and affordable emulator for the very expensive CFD solvers. The neural network model is trained with the storm track parameters used to drive the CFD solvers, and the output of the model is the time-series evolution of the predicted storm surge across multiple nodes within the spatial domain of interest. Once the model is trained, it can be deployed for further predictions based on new storm track inputs. The developed neural network model is a time-series model, a Long short-term memory, a variation of Recurrent Neural Network, which is enriched with Convolutional Neural Networks. The convolutional neural network is employed to capture the correlation of data spatially. Therefore, the temporal and spatial correlations of data are captured by the combination of the mentioned models, the ConvLSTM model. As the problem is a sequence to sequence time-series problem, an encoder-decoder ConvLSTM model is designed. Some other techniques in the process of model training are also employed to enrich the model performance. The results show the proposed convolutional recurrent neural network outperforms the Gaussian Process implementation for the examined synthetic storm database.

PhyCRNet: Physics-informed Convolutional-Recurrent Network for Solving Spatiotemporal PDEs

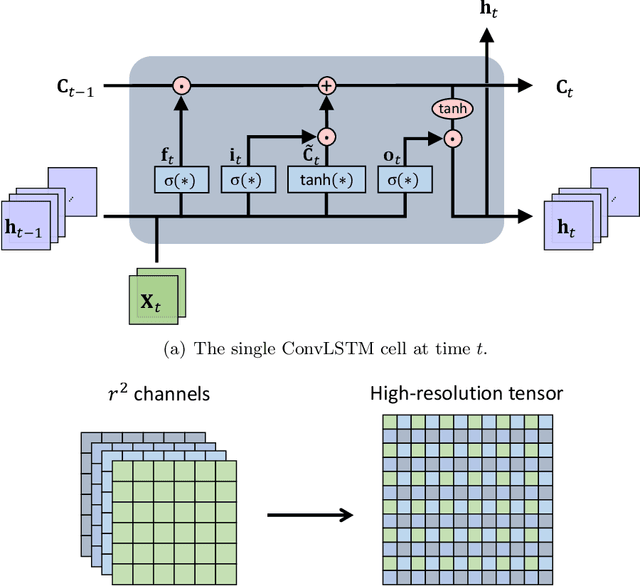
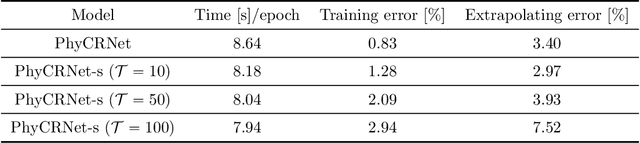
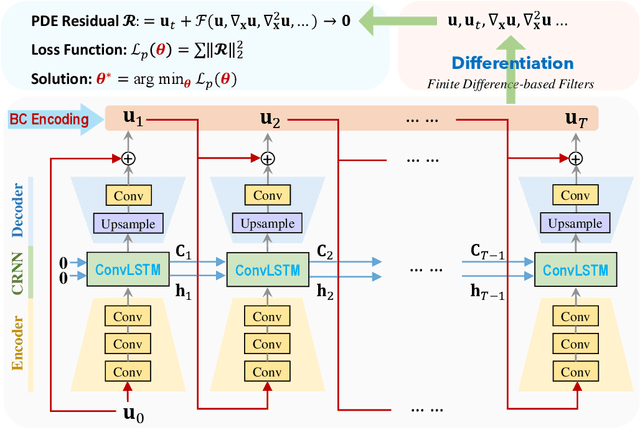
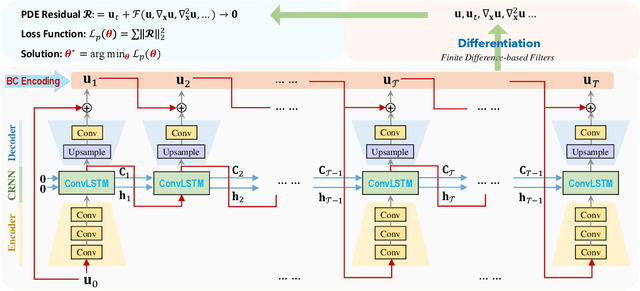
Partial differential equations (PDEs) play a fundamental role in modeling and simulating problems across a wide range of disciplines. Recent advances in deep learning have shown the great potential of physics-informed neural networks (PINNs) to solve PDEs as a basis for data-driven modeling and inverse analysis. However, the majority of existing PINN methods, based on fully-connected NNs, pose intrinsic limitations to low-dimensional spatiotemporal parameterizations. Moreover, since the initial/boundary conditions (I/BCs) are softly imposed via penalty, the solution quality heavily relies on hyperparameter tuning. To this end, we propose the novel physics-informed convolutional-recurrent learning architectures (PhyCRNet and PhyCRNet-s) for solving PDEs without any labeled data. Specifically, an encoder-decoder convolutional long short-term memory network is proposed for low-dimensional spatial feature extraction and temporal evolution learning. The loss function is defined as the aggregated discretized PDE residuals, while the I/BCs are hard-encoded in the network to ensure forcible satisfaction (e.g., periodic boundary padding). The networks are further enhanced by autoregressive and residual connections that explicitly simulate time marching. The performance of our proposed methods has been assessed by solving three nonlinear PDEs (e.g., 2D Burgers' equations, the $\lambda$-$\omega$ and FitzHugh Nagumo reaction-diffusion equations), and compared against the start-of-the-art baseline algorithms. The numerical results demonstrate the superiority of our proposed methodology in the context of solution accuracy, extrapolability and generalizability.