Chengping Rao
Physics-informed neural network for seismic wave inversion in layered semi-infinite domain
May 09, 2023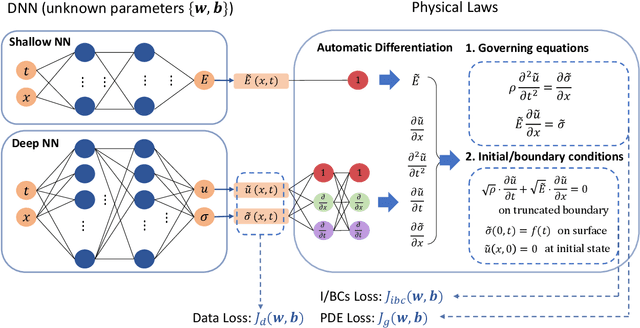

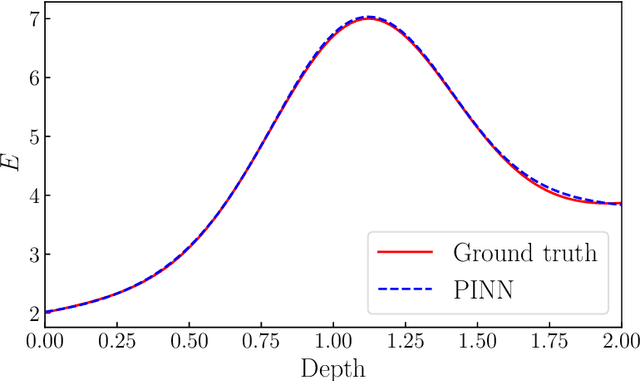
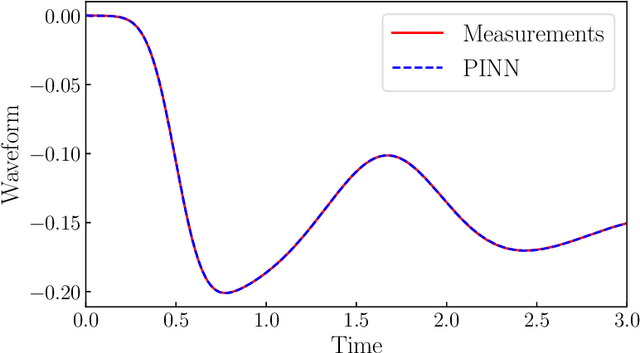
Abstract:Estimating the material distribution of Earth's subsurface is a challenging task in seismology and earthquake engineering. The recent development of physics-informed neural network (PINN) has shed new light on seismic inversion. In this paper, we present a PINN framework for seismic wave inversion in layered (1D) semi-infinite domain. The absorbing boundary condition is incorporated into the network as a soft regularizer for avoiding excessive computation. In specific, we design a lightweight network to learn the unknown material distribution and a deep neural network to approximate solution variables. The entire network is end-to-end and constrained by both sparse measurement data and the underlying physical laws (i.e., governing equations and initial/boundary conditions). Various experiments have been conducted to validate the effectiveness of our proposed approach for inverse modeling of seismic wave propagation in 1D semi-infinite domain.
SeismicNet: Physics-informed neural networks for seismic wave modeling in semi-infinite domain
Nov 02, 2022Abstract:There has been an increasing interest in integrating physics knowledge and machine learning for modeling dynamical systems. However, very limited studies have been conducted on seismic wave modeling tasks. A critical challenge is that these geophysical problems are typically defined in large domains (i.e., semi-infinite), which leads to high computational cost. In this paper, we present a novel physics-informed neural network (PINN) model for seismic wave modeling in semi-infinite domain without the nedd of labeled data. In specific, the absorbing boundary condition is introduced into the network as a soft regularizer for handling truncated boundaries. In terms of computational efficiency, we consider a sequential training strategy via temporal domain decomposition to improve the scalability of the network and solution accuracy. Moreover, we design a novel surrogate modeling strategy for parametric loading, which estimates the wave propagation in semin-infinite domain given the seismic loading at different locations. Various numerical experiments have been implemented to evaluate the performance of the proposed PINN model in the context of forward modeling of seismic wave propagation. In particular, we define diverse material distributions to test the versatility of this approach. The results demonstrate excellent solution accuracy under distinctive scenarios.
Physics-informed Deep Super-resolution for Spatiotemporal Data
Aug 02, 2022
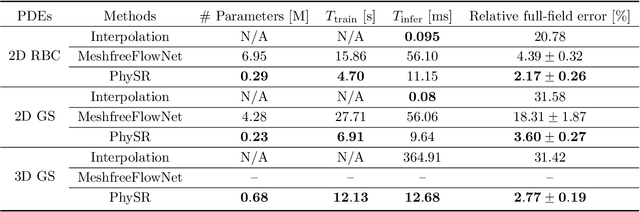


Abstract:High-fidelity simulation of complex physical systems is exorbitantly expensive and inaccessible across spatiotemporal scales. Recently, there has been an increasing interest in leveraging deep learning to augment scientific data based on the coarse-grained simulations, which is of cheap computational expense and retains satisfactory solution accuracy. However, the major existing work focuses on data-driven approaches which rely on rich training datasets and lack sufficient physical constraints. To this end, we propose a novel and efficient spatiotemporal super-resolution framework via physics-informed learning, inspired by the independence between temporal and spatial derivatives in partial differential equations (PDEs). The general principle is to leverage the temporal interpolation for flow estimation, and then introduce convolutional-recurrent neural networks for learning temporal refinement. Furthermore, we employ the stacked residual blocks with wide activation and sub-pixel layers with pixelshuffle for spatial reconstruction, where feature extraction is conducted in a low-resolution latent space. Moreover, we consider hard imposition of boundary conditions in the network to improve reconstruction accuracy. Results demonstrate the superior effectiveness and efficiency of the proposed method compared with baseline algorithms through extensive numerical experiments.
Discovering Nonlinear PDEs from Scarce Data with Physics-encoded Learning
Jan 28, 2022
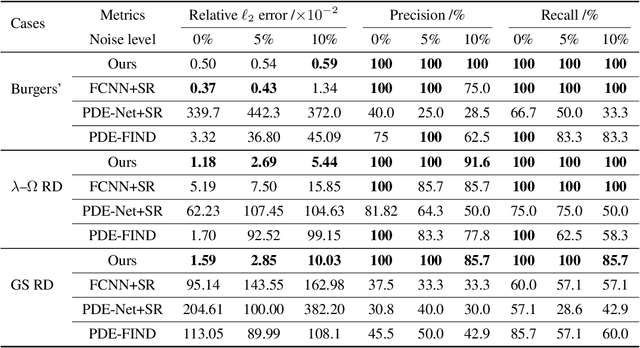
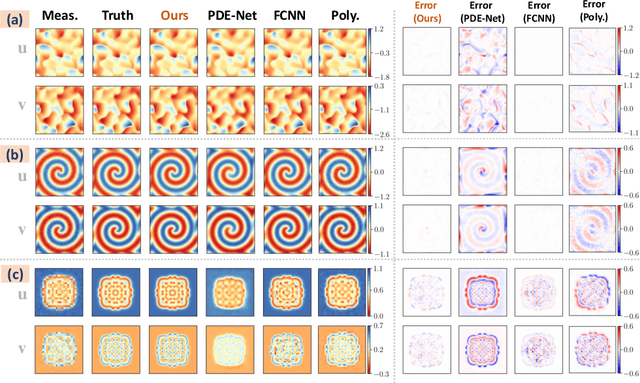

Abstract:There have been growing interests in leveraging experimental measurements to discover the underlying partial differential equations (PDEs) that govern complex physical phenomena. Although past research attempts have achieved great success in data-driven PDE discovery, the robustness of the existing methods cannot be guaranteed when dealing with low-quality measurement data. To overcome this challenge, we propose a novel physics-encoded discrete learning framework for discovering spatiotemporal PDEs from scarce and noisy data. The general idea is to (1) firstly introduce a novel deep convolutional-recurrent network, which can encode prior physics knowledge (e.g., known PDE terms, assumed PDE structure, initial/boundary conditions, etc.) while remaining flexible on representation capability, to accurately reconstruct high-fidelity data, and (2) perform sparse regression with the reconstructed data to identify the explicit form of the governing PDEs. We validate our method on three nonlinear PDE systems. The effectiveness and superiority of the proposed method over baseline models are demonstrated.
PhyCRNet: Physics-informed Convolutional-Recurrent Network for Solving Spatiotemporal PDEs
Jun 26, 2021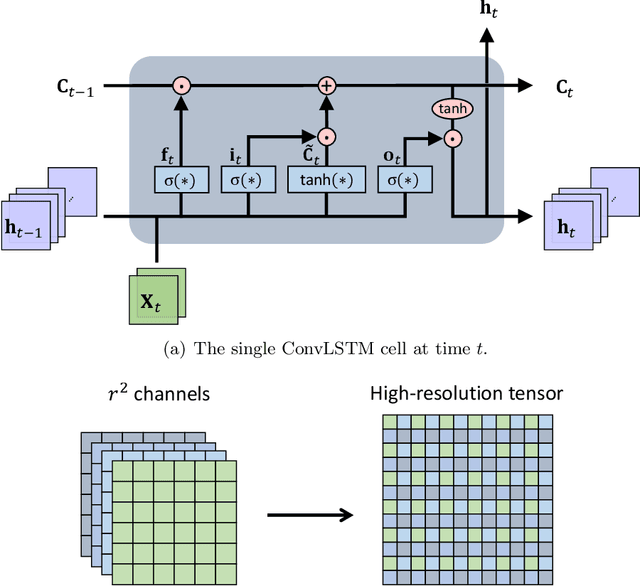
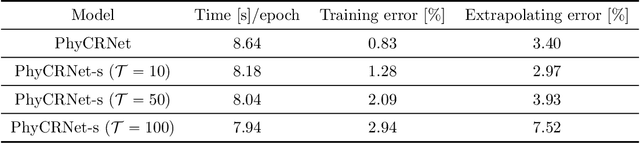
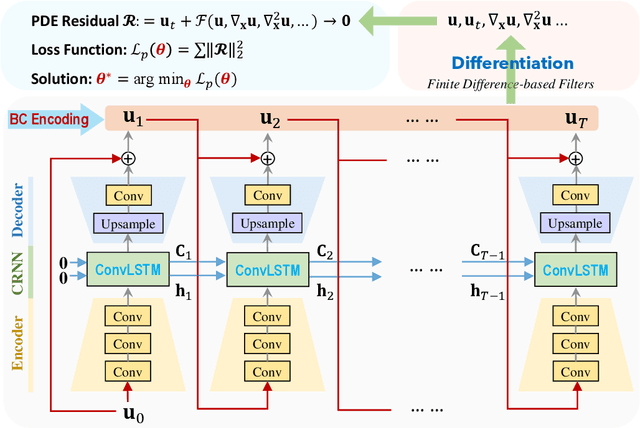
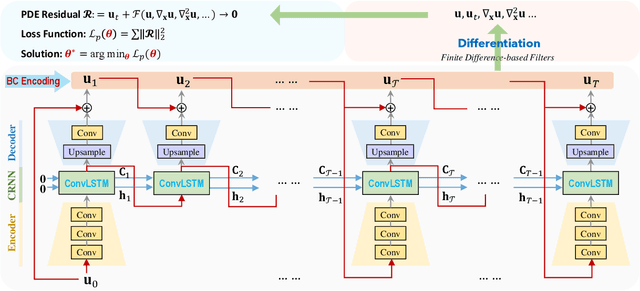
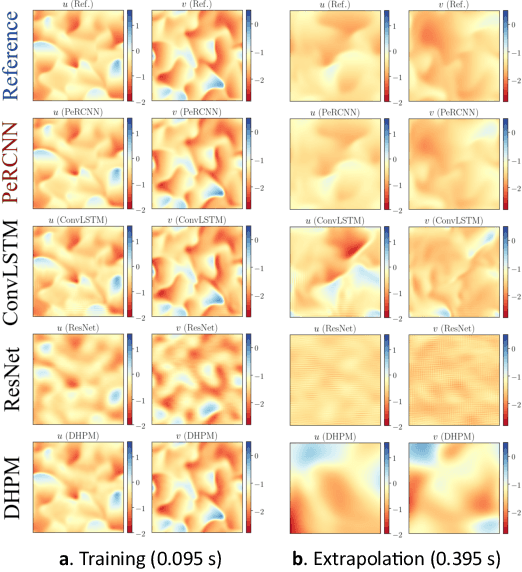
Abstract:Partial differential equations (PDEs) play a fundamental role in modeling and simulating problems across a wide range of disciplines. Recent advances in deep learning have shown the great potential of physics-informed neural networks (PINNs) to solve PDEs as a basis for data-driven modeling and inverse analysis. However, the majority of existing PINN methods, based on fully-connected NNs, pose intrinsic limitations to low-dimensional spatiotemporal parameterizations. Moreover, since the initial/boundary conditions (I/BCs) are softly imposed via penalty, the solution quality heavily relies on hyperparameter tuning. To this end, we propose the novel physics-informed convolutional-recurrent learning architectures (PhyCRNet and PhyCRNet-s) for solving PDEs without any labeled data. Specifically, an encoder-decoder convolutional long short-term memory network is proposed for low-dimensional spatial feature extraction and temporal evolution learning. The loss function is defined as the aggregated discretized PDE residuals, while the I/BCs are hard-encoded in the network to ensure forcible satisfaction (e.g., periodic boundary padding). The networks are further enhanced by autoregressive and residual connections that explicitly simulate time marching. The performance of our proposed methods has been assessed by solving three nonlinear PDEs (e.g., 2D Burgers' equations, the $\lambda$-$\omega$ and FitzHugh Nagumo reaction-diffusion equations), and compared against the start-of-the-art baseline algorithms. The numerical results demonstrate the superiority of our proposed methodology in the context of solution accuracy, extrapolability and generalizability.
Embedding Physics to Learn Spatiotemporal Dynamics from Sparse Data
Jun 09, 2021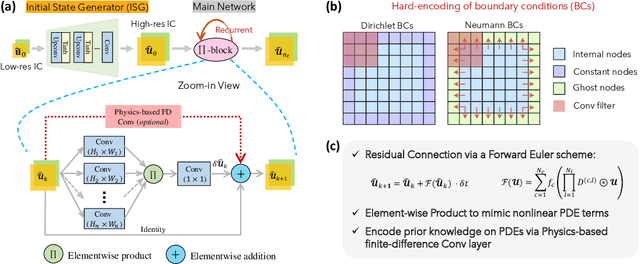
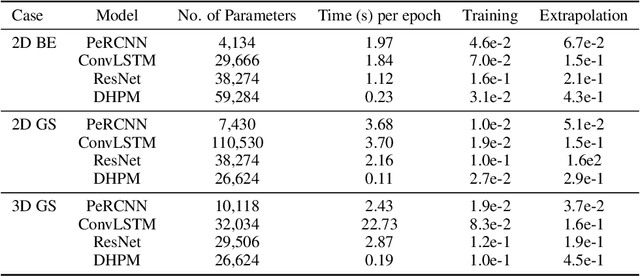
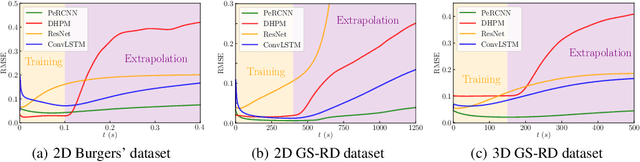
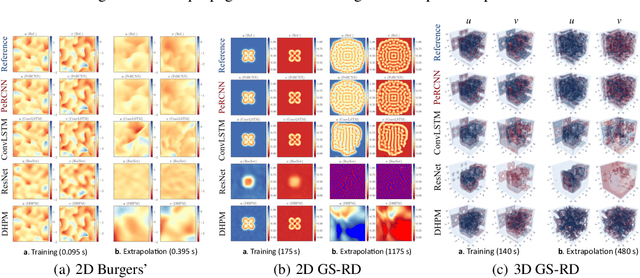
Abstract:Modeling nonlinear spatiotemporal dynamical systems has primarily relied on partial differential equations (PDEs) that are typically derived from first principles. However, the explicit formulation of PDEs for many underexplored processes, such as climate systems, biochemical reaction and epidemiology, remains uncertain or partially unknown, where very sparse measurement data is yet available. To tackle this challenge, we propose a novel deep learning architecture that forcibly embedded known physics knowledge in a residual-recurrent $\Pi$-block network, to facilitate the learning of the spatiotemporal dynamics in a data-driven manner. The coercive embedding mechanism of physics, fundamentally different from physics-informed neural networks based on loss penalty, ensures the network to rigorously obey given physics. Numerical experiments demonstrate that the resulting learning paradigm that embeds physics possesses remarkable accuracy, robustness, interpretability and generalizability for learning spatiotemporal dynamics.
Hard Encoding of Physics for Learning Spatiotemporal Dynamics
May 02, 2021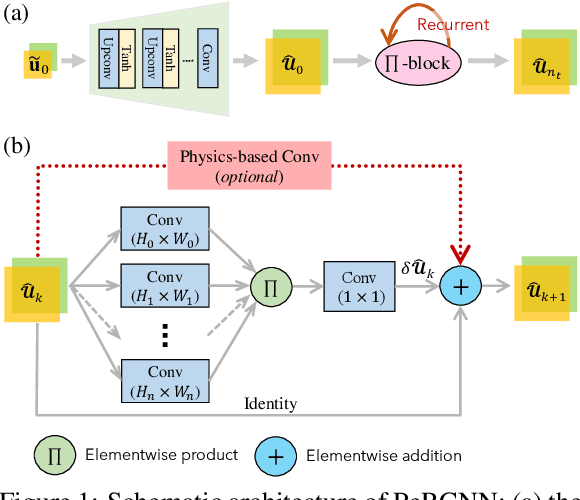


Abstract:Modeling nonlinear spatiotemporal dynamical systems has primarily relied on partial differential equations (PDEs). However, the explicit formulation of PDEs for many underexplored processes, such as climate systems, biochemical reaction and epidemiology, remains uncertain or partially unknown, where very limited measurement data is yet available. To tackle this challenge, we propose a novel deep learning architecture that forcibly encodes known physics knowledge to facilitate learning in a data-driven manner. The coercive encoding mechanism of physics, which is fundamentally different from the penalty-based physics-informed learning, ensures the network to rigorously obey given physics. Instead of using nonlinear activation functions, we propose a novel elementwise product operation to achieve the nonlinearity of the model. Numerical experiment demonstrates that the resulting physics-encoded learning paradigm possesses remarkable robustness against data noise/scarcity and generalizability compared with some state-of-the-art models for data-driven modeling.
Physics informed deep learning for computational elastodynamics without labeled data
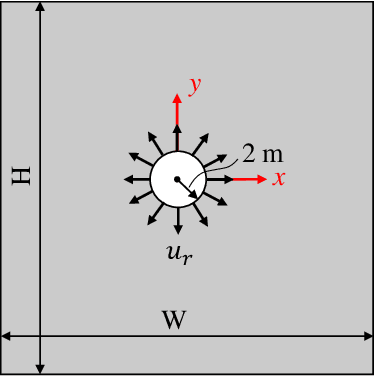
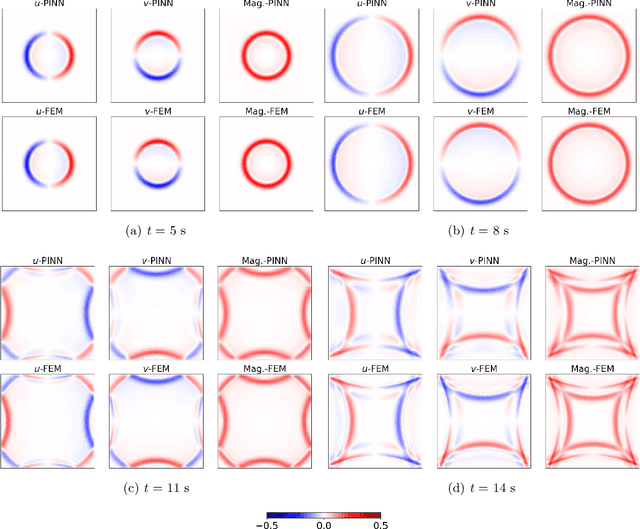
Jun 10, 2020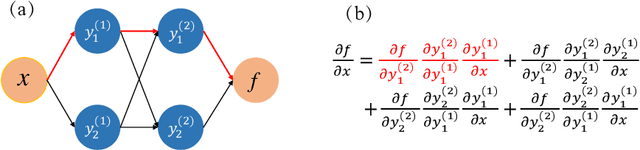

Abstract:Numerical methods such as finite element have been flourishing in the past decades for modeling solid mechanics problems via solving governing partial differential equations (PDEs). A salient aspect that distinguishes these numerical methods is how they approximate the physical fields of interest. Physics-informed deep learning is a novel approach recently developed for modeling PDE solutions and shows promise to solve computational mechanics problems without using any labeled data. The philosophy behind it is to approximate the quantity of interest (e.g., PDE solution variables) by a deep neural network (DNN) and embed the physical law to regularize the network. To this end, training the network is equivalent to minimization of a well-designed loss function that contains the PDE residuals and initial/boundary conditions (I/BCs). In this paper, we present a physics-informed neural network (PINN) with mixed-variable output to model elastodynamics problems without resort to labeled data, in which the I/BCs are hardly imposed. In particular, both the displacement and stress components are taken as the DNN output, inspired by the hybrid finite element analysis, which largely improves the accuracy and trainability of the network. Since the conventional PINN framework augments all the residual loss components in a "soft" manner with Lagrange multipliers, the weakly imposed I/BCs cannot not be well satisfied especially when complex I/BCs are present. To overcome this issue, a composite scheme of DNNs is established based on multiple single DNNs such that the I/BCs can be satisfied forcibly in a "hard" manner. The propose PINN framework is demonstrated on several numerical elasticity examples with different I/BCs, including both static and dynamic problems as well as wave propagation in truncated domains. Results show the promise of PINN in the context of computational mechanics applications.
Physics-informed deep learning for incompressible laminar flows
Feb 24, 2020
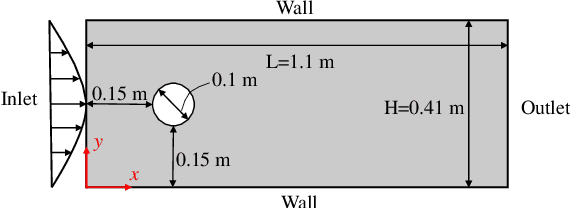
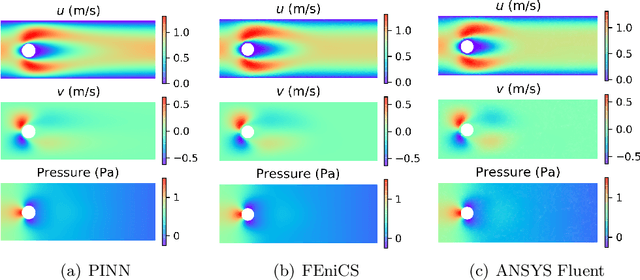

Abstract:Physics-informed deep learning (PIDL) has drawn tremendous interest in recent years to solve computational physics problems. The basic concept of PIDL is to embed available physical laws to constrain/inform neural networks, with the need of less rich data for training a reliable model. This can be achieved by incorporating the residual of the partial differential equations and the initial/boundary conditions into the loss function. Through minimizing the loss function, the neural network would be able to approximate the solution to the physical field of interest. In this paper, we propose a mixed-variable scheme of physics-informed neural network (PINN) for fluid dynamics and apply it to simulate steady and transient laminar flows at low Reynolds numbers. The predicted velocity and pressure fields by the proposed PINN approach are compared with the reference numerical solutions. Simulation results demonstrate great potential of the proposed PINN for fluid flow simulation with a high accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge