Hard Encoding of Physics for Learning Spatiotemporal Dynamics
Paper and Code
May 02, 2021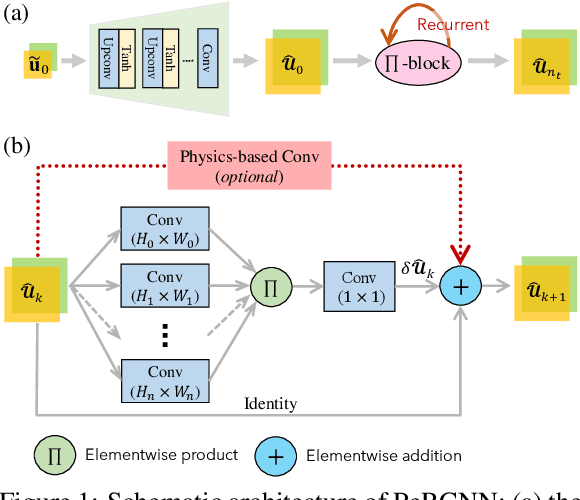

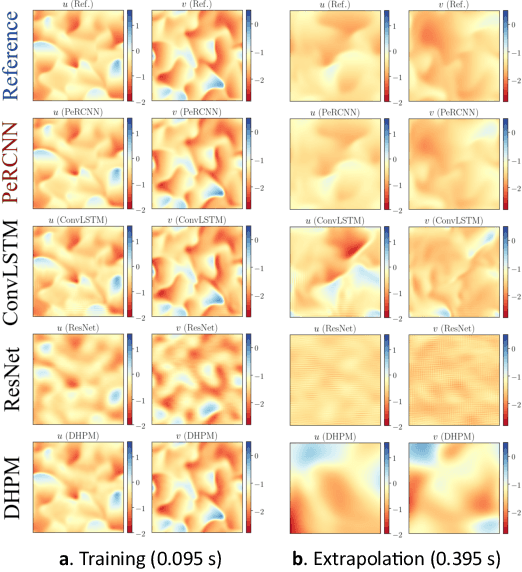

Modeling nonlinear spatiotemporal dynamical systems has primarily relied on partial differential equations (PDEs). However, the explicit formulation of PDEs for many underexplored processes, such as climate systems, biochemical reaction and epidemiology, remains uncertain or partially unknown, where very limited measurement data is yet available. To tackle this challenge, we propose a novel deep learning architecture that forcibly encodes known physics knowledge to facilitate learning in a data-driven manner. The coercive encoding mechanism of physics, which is fundamentally different from the penalty-based physics-informed learning, ensures the network to rigorously obey given physics. Instead of using nonlinear activation functions, we propose a novel elementwise product operation to achieve the nonlinearity of the model. Numerical experiment demonstrates that the resulting physics-encoded learning paradigm possesses remarkable robustness against data noise/scarcity and generalizability compared with some state-of-the-art models for data-driven modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge