Physics-informed Deep Super-resolution for Spatiotemporal Data
Paper and Code
Aug 02, 2022
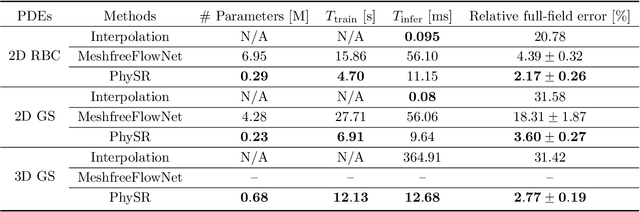


High-fidelity simulation of complex physical systems is exorbitantly expensive and inaccessible across spatiotemporal scales. Recently, there has been an increasing interest in leveraging deep learning to augment scientific data based on the coarse-grained simulations, which is of cheap computational expense and retains satisfactory solution accuracy. However, the major existing work focuses on data-driven approaches which rely on rich training datasets and lack sufficient physical constraints. To this end, we propose a novel and efficient spatiotemporal super-resolution framework via physics-informed learning, inspired by the independence between temporal and spatial derivatives in partial differential equations (PDEs). The general principle is to leverage the temporal interpolation for flow estimation, and then introduce convolutional-recurrent neural networks for learning temporal refinement. Furthermore, we employ the stacked residual blocks with wide activation and sub-pixel layers with pixelshuffle for spatial reconstruction, where feature extraction is conducted in a low-resolution latent space. Moreover, we consider hard imposition of boundary conditions in the network to improve reconstruction accuracy. Results demonstrate the superior effectiveness and efficiency of the proposed method compared with baseline algorithms through extensive numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge