Jiacheng He
ICH-Qwen: A Large Language Model Towards Chinese Intangible Cultural Heritage
May 28, 2025Abstract:The intangible cultural heritage (ICH) of China, a cultural asset transmitted across generations by various ethnic groups, serves as a significant testament to the evolution of human civilization and holds irreplaceable value for the preservation of historical lineage and the enhancement of cultural self-confidence. However, the rapid pace of modernization poses formidable challenges to ICH, including threats damage, disappearance and discontinuity of inheritance. China has the highest number of items on the UNESCO Intangible Cultural Heritage List, which is indicative of the nation's abundant cultural resources and emphasises the pressing need for ICH preservation. In recent years, the rapid advancements in large language modelling have provided a novel technological approach for the preservation and dissemination of ICH. This study utilises a substantial corpus of open-source Chinese ICH data to develop a large language model, ICH-Qwen, for the ICH domain. The model employs natural language understanding and knowledge reasoning capabilities of large language models, augmented with synthetic data and fine-tuning techniques. The experimental results demonstrate the efficacy of ICH-Qwen in executing tasks specific to the ICH domain. It is anticipated that the model will provide intelligent solutions for the protection, inheritance and dissemination of intangible cultural heritage, as well as new theoretical and practical references for the sustainable development of intangible cultural heritage. Furthermore, it is expected that the study will open up new paths for digital humanities research.
HyperGraph ROS: An Open-Source Robot Operating System for Hybrid Parallel Computing based on Computational HyperGraph
Mar 07, 2025



Abstract:This paper presents HyperGraph ROS, an open-source robot operating system that unifies intra-process, inter-process, and cross-device computation into a computational hypergraph for efficient message passing and parallel execution. In order to optimize communication, HyperGraph ROS dynamically selects the optimal communication mechanism while maintaining a consistent API. For intra-process messages, Intel-TBB Flow Graph is used with C++ pointer passing, which ensures zero memory copying and instant delivery. Meanwhile, inter-process and cross-device communication seamlessly switch to ZeroMQ. When a node receives a message from any source, it is immediately activated and scheduled for parallel execution by Intel-TBB. The computational hypergraph consists of nodes represented by TBB flow graph nodes and edges formed by TBB pointer-based connections for intra-process communication, as well as ZeroMQ links for inter-process and cross-device communication. This structure enables seamless distributed parallelism. Additionally, HyperGraph ROS provides ROS-like utilities such as a parameter server, a coordinate transformation tree, and visualization tools. Evaluation in diverse robotic scenarios demonstrates significantly higher transmission and throughput efficiency compared to ROS 2. Our work is available at https://github.com/wujiazheng2020a/hyper_graph_ros.
Mutual Information calculation on different appearances
Jul 10, 2024Abstract:Mutual information has many applications in image alignment and matching, mainly due to its ability to measure the statistical dependence between two images, even if the two images are from different modalities (e.g., CT and MRI). It considers not only the pixel intensities of the images but also the spatial relationships between the pixels. In this project, we apply the mutual information formula to image matching, where image A is the moving object and image B is the target object and calculate the mutual information between them to evaluate the similarity between the images. For comparison, we also used entropy and information-gain methods to test the dependency of the images. We also investigated the effect of different environments on the mutual information of the same image and used experiments and plots to demonstrate.
Variational Bayesian Approximations Kalman Filter Based on Threshold Judgment
Sep 22, 2023



Abstract:The estimation of non-Gaussian measurement noise models is a significant challenge across various fields. In practical applications, it often faces challenges due to the large number of parameters and high computational complexity. This paper proposes a threshold-based Kalman filtering approach for online estimation of noise parameters in non-Gaussian measurement noise models. This method uses a certain amount of sample data to infer the variance threshold of observation parameters and employs variational Bayesian estimation to obtain corresponding noise variance estimates, enabling subsequent iterations of the Kalman filtering algorithm. Finally, we evaluate the performance of this algorithm through simulation experiments, demonstrating its accurate and effective estimation of state and noise parameters.
A Covariance Adaptive Student's t Based Kalman Filter
Sep 18, 2023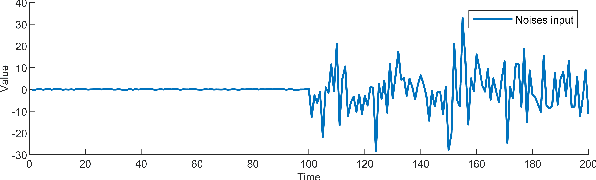
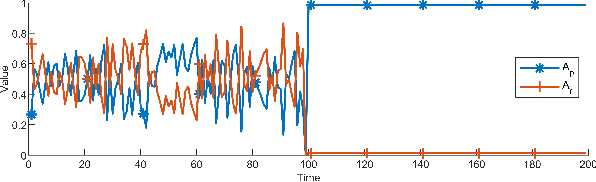
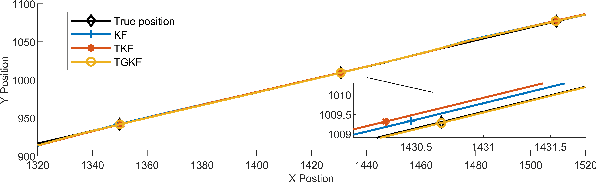
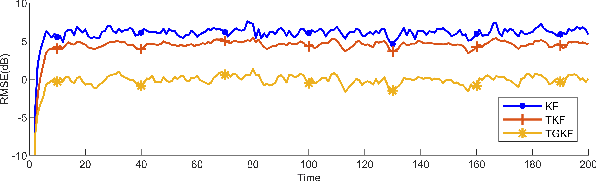
Abstract:In the classical Kalman filter(KF), the estimated state is a linear combination of the one-step predicted state and measurement state, their confidence level change when the prediction mean square error matrix and covariance matrix of measurement noise vary. The existing student's t based Kalman filter(TKF) works similarly to the way KF works, they both work well with impulse noise, but when it comes to Gaussian noise, TKF encounters an adjustment limit of the confidence level, this can lead to inaccuracies in such situations. This brief optimizes TKF by using the Gaussian mixture model(GMM), which generates a reasonable covariance matrix from the measurement noise to replace the one used in the existing algorithm and breaks the adjustment limit of the confidence level. At the end of the brief, the performance of the covariance adaptive student's t based Kalman filter(TGKF) is verified.
Distributed fusion filter over lossy wireless sensor networks with the presence of non-Gaussian noise
Jul 07, 2023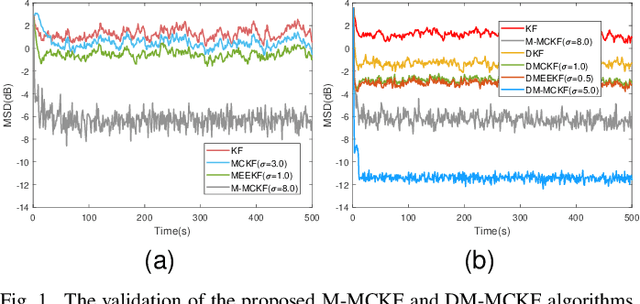
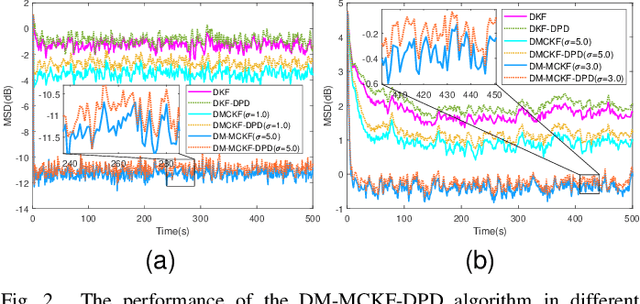
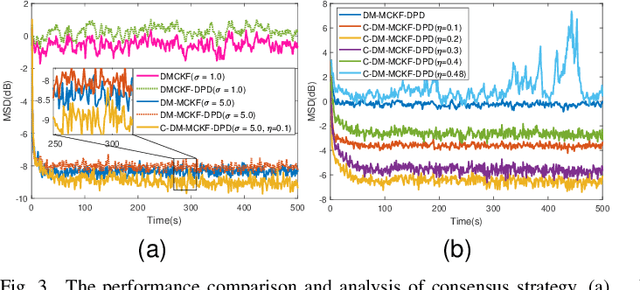
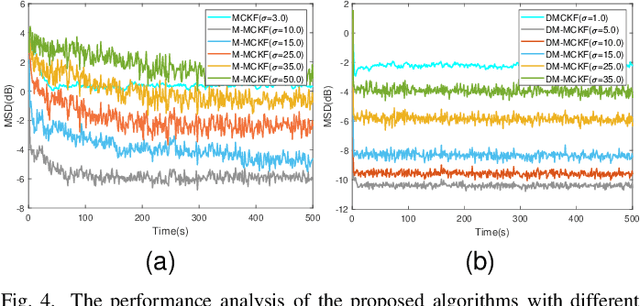
Abstract:The information transmission between nodes in a wireless sensor networks (WSNs) often causes packet loss due to denial-of-service (DoS) attack, energy limitations, and environmental factors, and the information that is successfully transmitted can also be contaminated by non-Gaussian noise. The presence of these two factors poses a challenge for distributed state estimation (DSE) over WSNs. In this paper, a generalized packet drop model is proposed to describe the packet loss phenomenon caused by DoS attacks and other factors. Moreover, a modified maximum correntropy Kalman filter is given, and it is extended to distributed form (DM-MCKF). In addition, a distributed modified maximum correntropy Kalman filter incorporating the generalized data packet drop (DM-MCKF-DPD) algorithm is provided to implement DSE with the presence of both non-Gaussian noise pollution and packet drop. A sufficient condition to ensure the convergence of the fixed-point iterative process of the DM-MCKF-DPD algorithm is presented and the computational complexity of the DM-MCKF-DPD algorithm is analyzed. Finally, the effectiveness and feasibility of the proposed algorithms are verified by simulations.
Quantized generalized minimum error entropy for kernel recursive least squares adaptive filtering
Jul 04, 2023



Abstract:The robustness of the kernel recursive least square (KRLS) algorithm has recently been improved by combining them with more robust information-theoretic learning criteria, such as minimum error entropy (MEE) and generalized MEE (GMEE), which also improves the computational complexity of the KRLS-type algorithms to a certain extent. To reduce the computational load of the KRLS-type algorithms, the quantized GMEE (QGMEE) criterion, in this paper, is combined with the KRLS algorithm, and as a result two kinds of KRLS-type algorithms, called quantized kernel recursive MEE (QKRMEE) and quantized kernel recursive GMEE (QKRGMEE), are designed. As well, the mean error behavior, mean square error behavior, and computational complexity of the proposed algorithms are investigated. In addition, simulation and real experimental data are utilized to verify the feasibility of the proposed algorithms.
A Model Fusion Distributed Kalman Filter For Non-Gaussian Observation Noise
Jun 20, 2023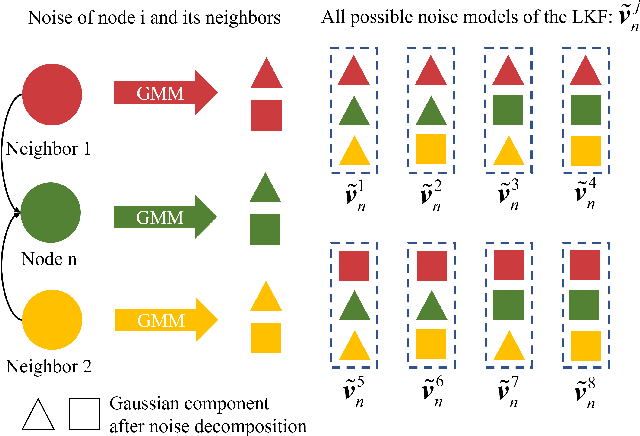
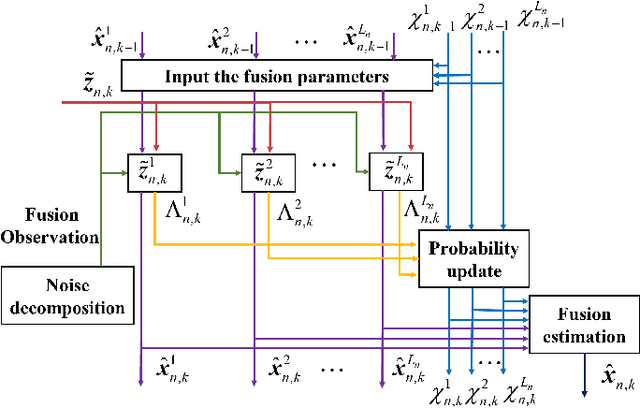
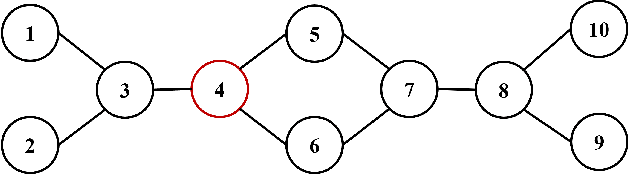
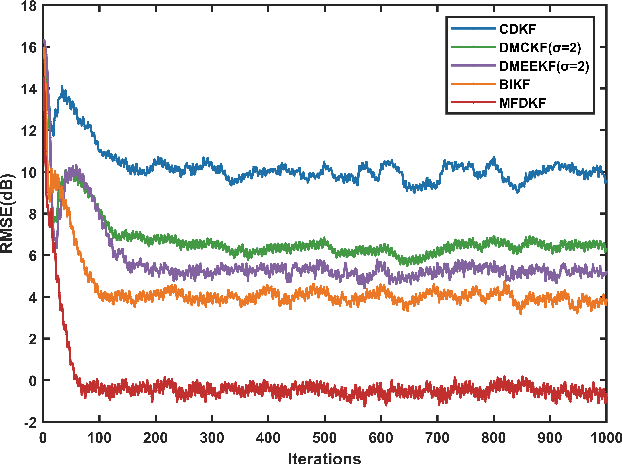
Abstract:The distributed Kalman filter (DKF) has attracted extensive research as an information fusion method for wireless sensor systems(WSNs). And the DKF in non-Gaussian environments is still a pressing problem. In this paper, we approximate the non-Gaussian noise as a Gaussian mixture model and estimate the parameters through the expectation-maximization algorithm. A DKF, called model fusion DKF (MFDKF) is proposed against the non-Gaussain noise. Specifically, the proposed MFDKF is obtained by fusing the sub-models that are built based on the noise approximation with the help of interacting multiple model (IMM). Considering that some WSNs demand high consensus or have restricted communication, consensus MFDKF (C-MFDKF) and simplified MFDKF (S-MFDKF) are proposed based on consensus theory, respectively. The convergence of MFDKF and its derivative algorithms are analyzed. A series of simulations indicate the effectiveness of the MFDKF and its derivative algorithms.
Minimum Error Entropy Rauch-Tung-Striebel Smoother
Jan 14, 2023Abstract:Outliers and impulsive disturbances often cause heavy-tailed distributions in practical applications, and these will degrade the performance of Gaussian approximation smoothing algorithms. To improve the robustness of the Rauch-Tung-Striebel (RTS) smother against complicated non-Gaussian noises, a new RTS-smoother integrated with the minimum error entropy (MEE) criterion (MEE-RTS) is proposed for linear systems, which is also extended to the state estimation of nonlinear systems by utilizing the Taylor series linearization approach. The mean error behavior, the mean square error behavior, as well as the computational complexity of the MEE-RTS smoother are analyzed. According to simulation results, the proposed smoothers perform better than several robust solutions in terms of steady-state error.
State Estimation of Wireless Sensor Networks in the Presence of Data Packet Drops and Non-Gaussian Noise
Jan 14, 2023
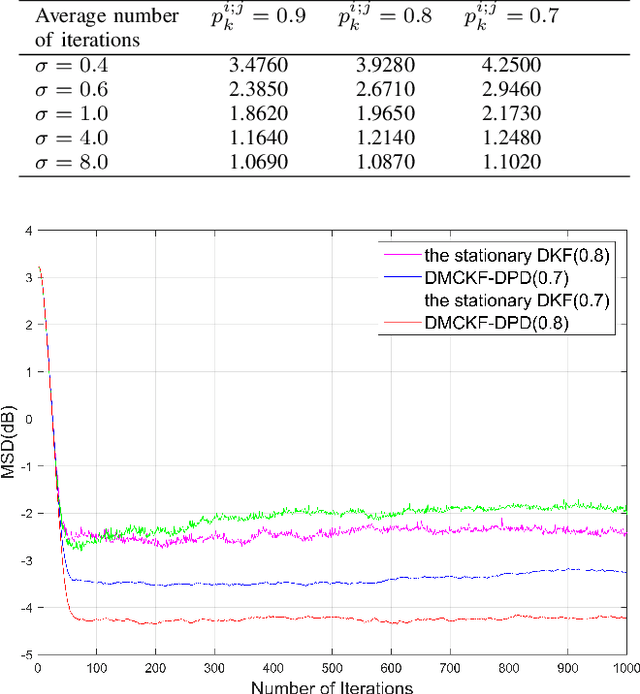


Abstract:Distributed Kalman filter approaches based on the maximum correntropy criterion have recently demonstrated superior state estimation performance to that of conventional distributed Kalman filters for wireless sensor networks in the presence of non-Gaussian impulsive noise. However, these algorithms currently fail to take account of data packet drops. The present work addresses this issue by proposing a distributed maximum correntropy Kalman filter that accounts for data packet drops (i.e., the DMCKF-DPD algorithm). The effectiveness and feasibility of the algorithm are verified by simulations conducted in a wireless sensor network with intermittent observations due to data packet drops under a non-Gaussian noise environment. Moreover, the computational complexity of the DMCKF-DPD algorithm is demonstrated to be moderate compared with that of a conventional distributed Kalman filter, and we provide a sufficient condition to ensure the convergence of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge