A Model Fusion Distributed Kalman Filter For Non-Gaussian Observation Noise
Paper and Code
Jun 20, 2023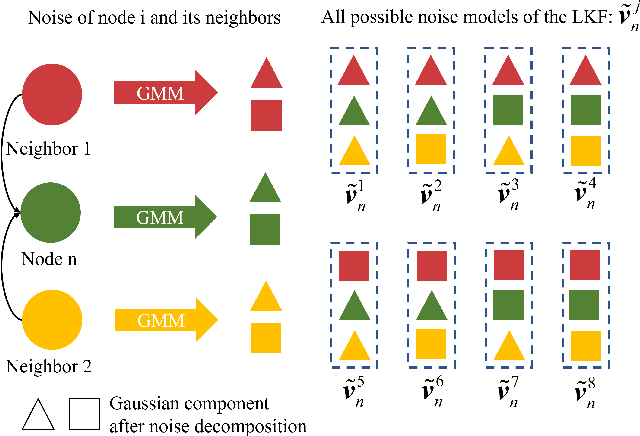
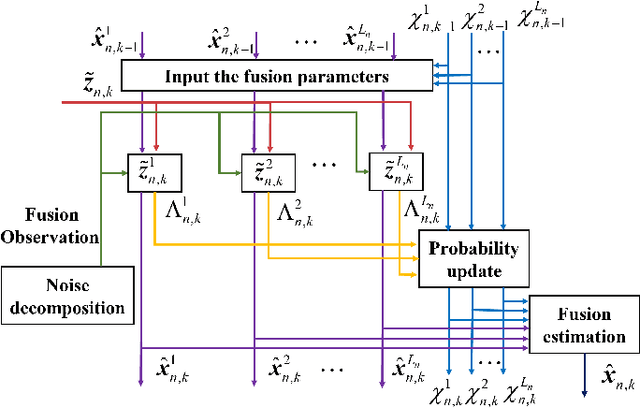
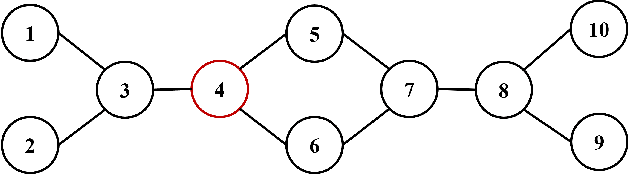
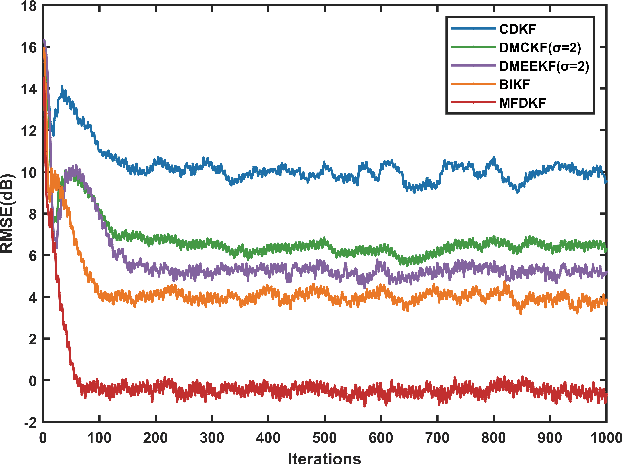
The distributed Kalman filter (DKF) has attracted extensive research as an information fusion method for wireless sensor systems(WSNs). And the DKF in non-Gaussian environments is still a pressing problem. In this paper, we approximate the non-Gaussian noise as a Gaussian mixture model and estimate the parameters through the expectation-maximization algorithm. A DKF, called model fusion DKF (MFDKF) is proposed against the non-Gaussain noise. Specifically, the proposed MFDKF is obtained by fusing the sub-models that are built based on the noise approximation with the help of interacting multiple model (IMM). Considering that some WSNs demand high consensus or have restricted communication, consensus MFDKF (C-MFDKF) and simplified MFDKF (S-MFDKF) are proposed based on consensus theory, respectively. The convergence of MFDKF and its derivative algorithms are analyzed. A series of simulations indicate the effectiveness of the MFDKF and its derivative algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge