Distributed fusion filter over lossy wireless sensor networks with the presence of non-Gaussian noise

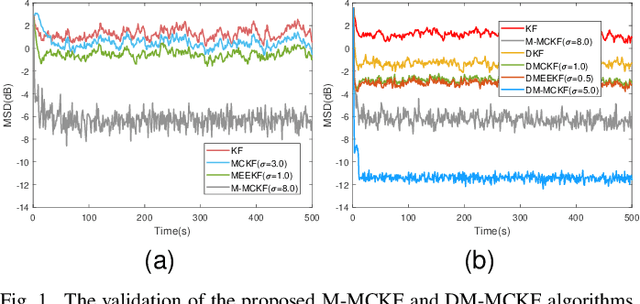
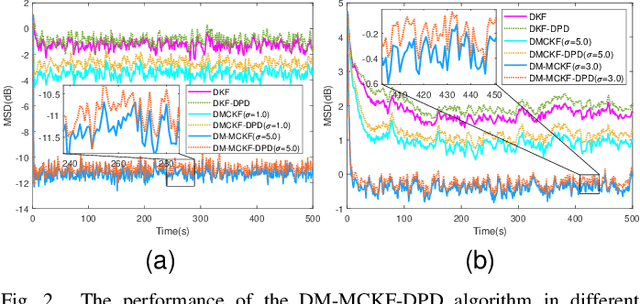
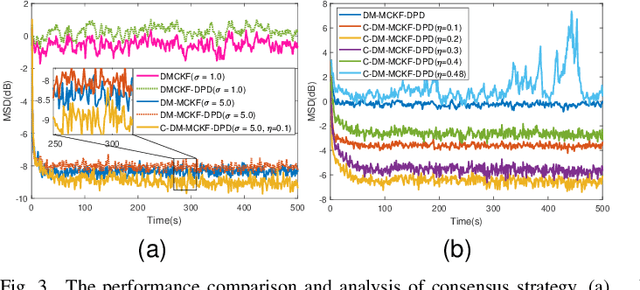
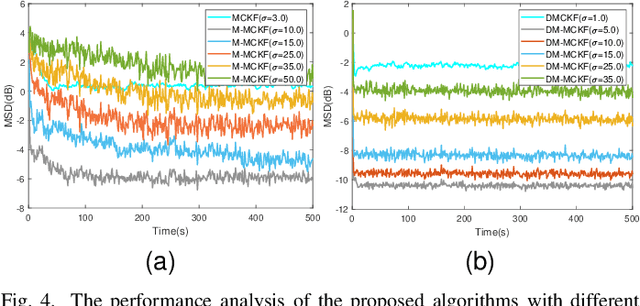
The information transmission between nodes in a wireless sensor networks (WSNs) often causes packet loss due to denial-of-service (DoS) attack, energy limitations, and environmental factors, and the information that is successfully transmitted can also be contaminated by non-Gaussian noise. The presence of these two factors poses a challenge for distributed state estimation (DSE) over WSNs. In this paper, a generalized packet drop model is proposed to describe the packet loss phenomenon caused by DoS attacks and other factors. Moreover, a modified maximum correntropy Kalman filter is given, and it is extended to distributed form (DM-MCKF). In addition, a distributed modified maximum correntropy Kalman filter incorporating the generalized data packet drop (DM-MCKF-DPD) algorithm is provided to implement DSE with the presence of both non-Gaussian noise pollution and packet drop. A sufficient condition to ensure the convergence of the fixed-point iterative process of the DM-MCKF-DPD algorithm is presented and the computational complexity of the DM-MCKF-DPD algorithm is analyzed. Finally, the effectiveness and feasibility of the proposed algorithms are verified by simulations.

Generalized Minimum Error Entropy for Adaptive Filtering

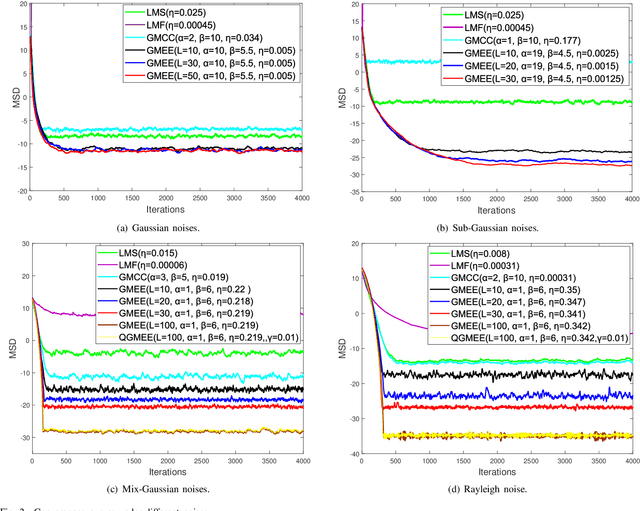
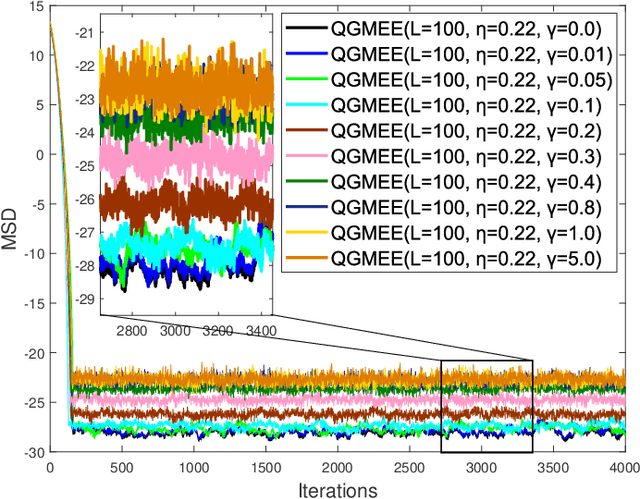
Error entropy is a important nonlinear similarity measure, and it has received increasing attention in many practical applications. The default kernel function of error entropy criterion is Gaussian kernel function, however, which is not always the best choice. In our study, a novel concept, called generalized error entropy, utilizing the generalized Gaussian density (GGD) function as the kernel function is proposed. We further derivate the generalized minimum error entropy (GMEE) criterion, and a novel adaptive filtering called GMEE algorithm is derived by utilizing GMEE criterion. The stability, steady-state performance, and computational complexity of the proposed algorithm are investigated. Some simulation indicate that the GMEE algorithm performs well in Gaussian, sub-Gaussian, and super-Gaussian noises environment, respectively. Finally, the GMEE algorithm is applied to acoustic echo cancelation and performs well.