Jia Lu
WorldGrow: Generating Infinite 3D World
Oct 24, 2025



Abstract:We tackle the challenge of generating the infinitely extendable 3D world -- large, continuous environments with coherent geometry and realistic appearance. Existing methods face key challenges: 2D-lifting approaches suffer from geometric and appearance inconsistencies across views, 3D implicit representations are hard to scale up, and current 3D foundation models are mostly object-centric, limiting their applicability to scene-level generation. Our key insight is leveraging strong generation priors from pre-trained 3D models for structured scene block generation. To this end, we propose WorldGrow, a hierarchical framework for unbounded 3D scene synthesis. Our method features three core components: (1) a data curation pipeline that extracts high-quality scene blocks for training, making the 3D structured latent representations suitable for scene generation; (2) a 3D block inpainting mechanism that enables context-aware scene extension; and (3) a coarse-to-fine generation strategy that ensures both global layout plausibility and local geometric/textural fidelity. Evaluated on the large-scale 3D-FRONT dataset, WorldGrow achieves SOTA performance in geometry reconstruction, while uniquely supporting infinite scene generation with photorealistic and structurally consistent outputs. These results highlight its capability for constructing large-scale virtual environments and potential for building future world models.
Snap-Snap: Taking Two Images to Reconstruct 3D Human Gaussians in Milliseconds
Aug 20, 2025Abstract:Reconstructing 3D human bodies from sparse views has been an appealing topic, which is crucial to broader the related applications. In this paper, we propose a quite challenging but valuable task to reconstruct the human body from only two images, i.e., the front and back view, which can largely lower the barrier for users to create their own 3D digital humans. The main challenges lie in the difficulty of building 3D consistency and recovering missing information from the highly sparse input. We redesign a geometry reconstruction model based on foundation reconstruction models to predict consistent point clouds even input images have scarce overlaps with extensive human data training. Furthermore, an enhancement algorithm is applied to supplement the missing color information, and then the complete human point clouds with colors can be obtained, which are directly transformed into 3D Gaussians for better rendering quality. Experiments show that our method can reconstruct the entire human in 190 ms on a single NVIDIA RTX 4090, with two images at a resolution of 1024x1024, demonstrating state-of-the-art performance on the THuman2.0 and cross-domain datasets. Additionally, our method can complete human reconstruction even with images captured by low-cost mobile devices, reducing the requirements for data collection. Demos and code are available at https://hustvl.github.io/Snap-Snap/.
You Only Acquire Sparse-channel (YOAS): A Unified Framework for Dense-channel EEG Generation
Jun 21, 2024



Abstract:High-precision acquisition of dense-channel electroencephalogram (EEG) signals is often impeded by the costliness and lack of portability of equipment. In contrast, generating dense-channel EEG signals effectively from sparse channels shows promise and economic viability. However, sparse-channel EEG poses challenges such as reduced spatial resolution, information loss, signal mixing, and heightened susceptibility to noise and interference. To address these challenges, we first theoretically formulate the dense-channel EEG generation problem as by optimizing a set of cross-channel EEG signal generation problems. Then, we propose the YOAS framework for generating dense-channel data from sparse-channel EEG signals. The YOAS totally consists of four sequential stages: Data Preparation, Data Preprocessing, Biased-EEG Generation, and Synthetic EEG Generation. Data Preparation and Preprocessing carefully consider the distribution of EEG electrodes and low signal-to-noise ratio problem of EEG signals. Biased-EEG Generation includes sub-modules of BiasEEGGanFormer and BiasEEGDiffFormer, which facilitate long-term feature extraction with attention and generate signals by combining electrode position alignment with diffusion model, respectively. Synthetic EEG Generation synthesizes the final signals, employing a deduction paradigm for multi-channel EEG generation. Extensive experiments confirmed YOAS's feasibility, efficiency, and theoretical validity, even remarkably enhancing data discernibility. This breakthrough in dense-channel EEG signal generation from sparse-channel data opens new avenues for exploration in EEG signal processing and application.
MLPSVM:A new parallel support vector machine to multi-label learning
Apr 13, 2020
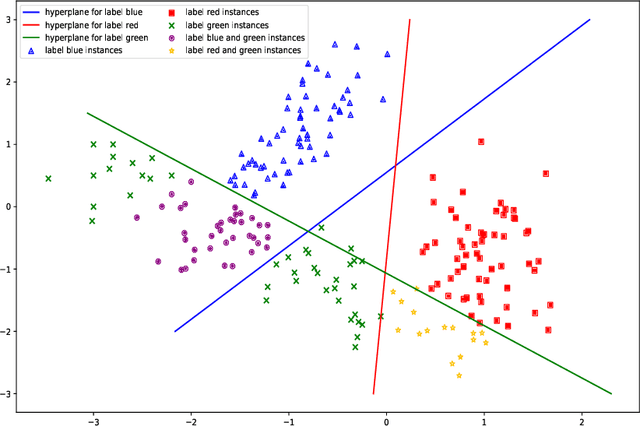
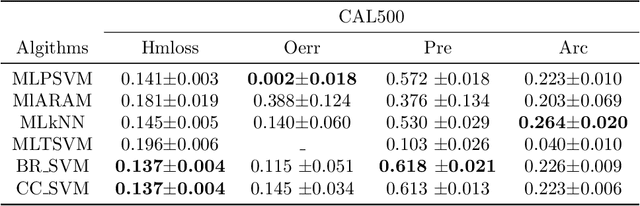
Abstract:Multi-label learning has attracted the attention of the machine learning community. The problem conversion method Binary Relevance converts a familiar single label into a multi-label algorithm. The binary relevance method is widely used because of its simple structure and efficient algorithm. But binary relevance does not consider the links between labels, making it cumbersome to handle some tasks. This paper proposes a multi-label learning algorithm that can also be used for single-label classification. It is based on standard support vector machines and changes the original single decision hyperplane into two parallel decision hyper-planes, which call multi-label parallel support vector machine (MLPSVM). At the end of the article, MLPSVM is compared with other multi-label learning algorithms. The experimental results show that the algorithm performs well on data sets.
ZerNet: Convolutional Neural Networks on Arbitrary Surfaces via Zernike Local Tangent Space Estimation
Dec 03, 2018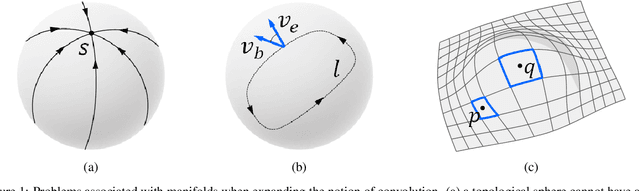
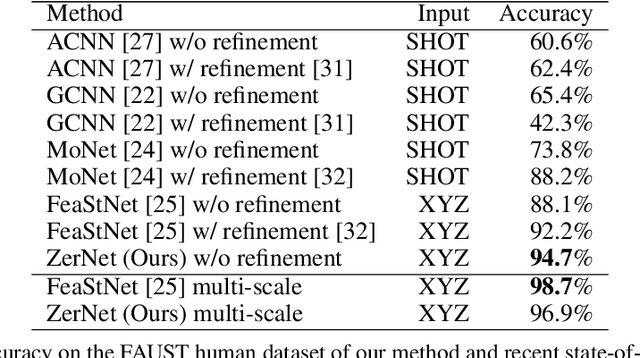
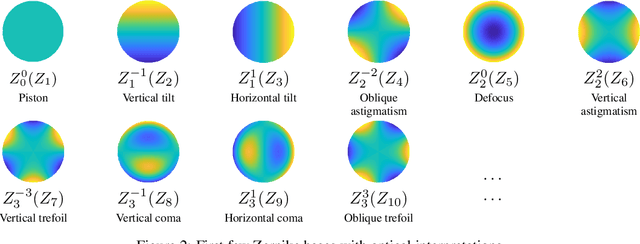
Abstract:The research community has observed a massive success of convolutional neural networks (CNN) in visual recognition tasks. Such powerful CNNs, however, do not generalize well to arbitrary-shaped mainfold domains. Thus, still many visual recognition problems defined on arbitrary manifolds cannot benefit much from the success of CNNs, if at all. Technical difficulties hindering generalization of CNNs are rooted in the lack of a canonical grid-like representation, the notion of consistent orientation, and a compatible local topology across the domain. Unfortunately, except for a few pioneering works, only very little has been studied in this regard. To this end, in this paper, we propose a novel mathematical formulation to extend CNNs onto two-dimensional (2D) manifold domains. More specifically, we approximate a tensor field defined over a manifold using orthogonal basis functions, called Zernike polynomials, on local tangent spaces. We prove that the convolution of two functions can be represented as a simple dot product between Zernike polynomial coefficients. We also prove that a rotation of a convolution kernel equates to a 2 by 2 rotation matrix applied to Zernike polynomial coefficients, which can be critical in manifold domains. As such, the key contribution of this work resides in a concise but rigorous mathematical generalization of the CNN building blocks. Furthermore, comparative to the other state-of-the-art methods, our method demonstrates substantially better performance on both classification and regression tasks.
Wall Stress Estimation of Cerebral Aneurysm based on Zernike Convolutional Neural Networks
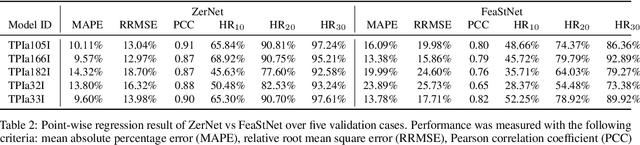
Jun 20, 2018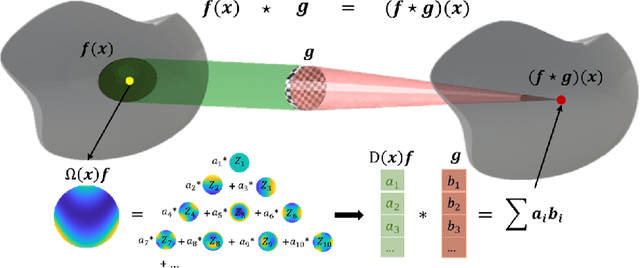
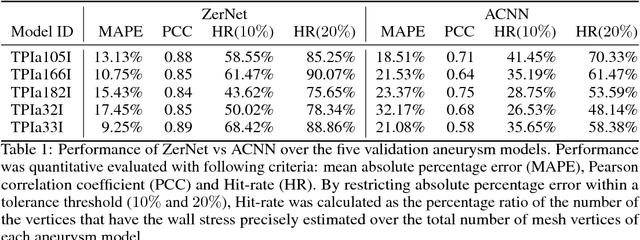
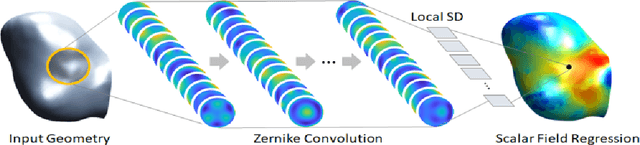
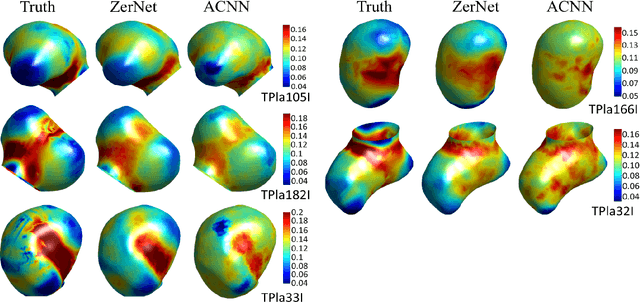
Abstract:Convolutional neural networks (ConvNets) have demonstrated an exceptional capacity to discern visual patterns from digital images and signals. Unfortunately, such powerful ConvNets do not generalize well to arbitrary-shaped manifolds, where data representation does not fit into a tensor-like grid. Hence, many fields of science and engineering, where data points possess some manifold structure, cannot enjoy the full benefits of the recent advances in ConvNets. The aneurysm wall stress estimation problem introduced in this paper is one of many such problems. The problem is well-known to be of a paramount clinical importance, but yet, traditional ConvNets cannot be applied due to the manifold structure of the data, neither does the state-of-the-art geometric ConvNets perform well. Motivated by this, we propose a new geometric ConvNet method named ZerNet, which builds upon our novel mathematical generalization of convolution and pooling operations on manifolds. Our study shows that the ZerNet outperforms the other state-of-the-art geometric ConvNets in terms of accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge