Single-cell Curriculum Learning-based Deep Graph Embedding Clustering

The swift advancement of single-cell RNA sequencing (scRNA-seq) technologies enables the investigation of cellular-level tissue heterogeneity. Cell annotation significantly contributes to the extensive downstream analysis of scRNA-seq data. However, The analysis of scRNA-seq for biological inference presents challenges owing to its intricate and indeterminate data distribution, characterized by a substantial volume and a high frequency of dropout events. Furthermore, the quality of training samples varies greatly, and the performance of the popular scRNA-seq data clustering solution GNN could be harmed by two types of low-quality training nodes: 1) nodes on the boundary; 2) nodes that contribute little additional information to the graph. To address these problems, we propose a single-cell curriculum learning-based deep graph embedding clustering (scCLG). We first propose a Chebyshev graph convolutional autoencoder with multi-decoder (ChebAE) that combines three optimization objectives corresponding to three decoders, including topology reconstruction loss of cell graphs, zero-inflated negative binomial (ZINB) loss, and clustering loss, to learn cell-cell topology representation. Meanwhile, we employ a selective training strategy to train GNN based on the features and entropy of nodes and prune the difficult nodes based on the difficulty scores to keep the high-quality graph. Empirical results on a variety of gene expression datasets show that our model outperforms state-of-the-art methods.

Noise-to-Norm Reconstruction for Industrial Anomaly Detection and Localization

Anomaly detection has a wide range of applications and is especially important in industrial quality inspection. Currently, many top-performing anomaly-detection models rely on feature-embedding methods. However, these methods do not perform well on datasets with large variations in object locations. Reconstruction-based methods use reconstruction errors to detect anomalies without considering positional differences between samples. In this study, a reconstruction-based method using the noise-to-norm paradigm is proposed, which avoids the invariant reconstruction of anomalous regions. Our reconstruction network is based on M-net and incorporates multiscale fusion and residual attention modules to enable end-to-end anomaly detection and localization. Experiments demonstrate that the method is effective in reconstructing anomalous regions into normal patterns and achieving accurate anomaly detection and localization. On the MPDD and VisA datasets, our proposed method achieved more competitive results than the latest methods, and it set a new state-of-the-art standard on the MPDD dataset.

ZerNet: Convolutional Neural Networks on Arbitrary Surfaces via Zernike Local Tangent Space Estimation

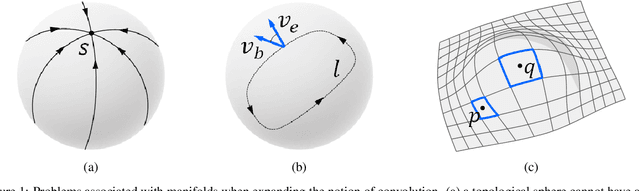
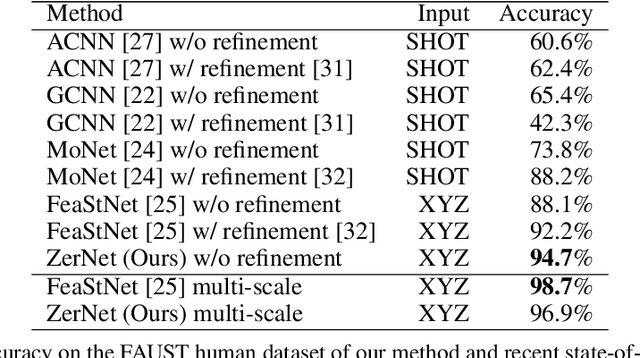
The research community has observed a massive success of convolutional neural networks (CNN) in visual recognition tasks. Such powerful CNNs, however, do not generalize well to arbitrary-shaped mainfold domains. Thus, still many visual recognition problems defined on arbitrary manifolds cannot benefit much from the success of CNNs, if at all. Technical difficulties hindering generalization of CNNs are rooted in the lack of a canonical grid-like representation, the notion of consistent orientation, and a compatible local topology across the domain. Unfortunately, except for a few pioneering works, only very little has been studied in this regard. To this end, in this paper, we propose a novel mathematical formulation to extend CNNs onto two-dimensional (2D) manifold domains. More specifically, we approximate a tensor field defined over a manifold using orthogonal basis functions, called Zernike polynomials, on local tangent spaces. We prove that the convolution of two functions can be represented as a simple dot product between Zernike polynomial coefficients. We also prove that a rotation of a convolution kernel equates to a 2 by 2 rotation matrix applied to Zernike polynomial coefficients, which can be critical in manifold domains. As such, the key contribution of this work resides in a concise but rigorous mathematical generalization of the CNN building blocks. Furthermore, comparative to the other state-of-the-art methods, our method demonstrates substantially better performance on both classification and regression tasks.

Deep Spectral Descriptors: Learning the point-wise correspondence metric via Siamese deep neural networks

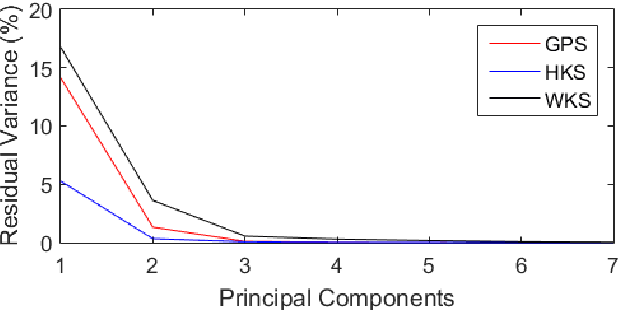
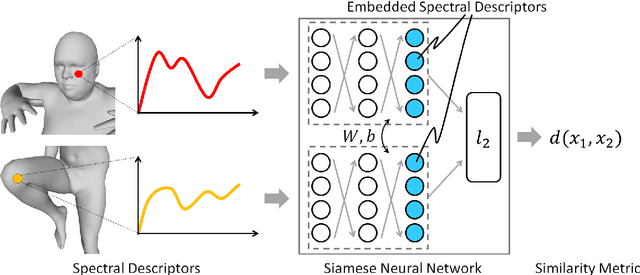
A robust and informative local shape descriptor plays an important role in mesh registration. In this regard, spectral descriptors that are based on the spectrum of the Laplace-Beltrami operator have gained a spotlight among the researchers for the last decade due to their desirable properties, such as isometry invariance. Despite such, however, spectral descriptors often fail to give a correct similarity measure for non-isometric cases where the metric distortion between the models is large. Hence, they are in general not suitable for the registration problems, except for the special cases when the models are near-isometry. In this paper, we investigate a way to develop shape descriptors for non-isometric registration tasks by embedding the spectral shape descriptors into a different metric space where the Euclidean distance between the elements directly indicates the geometric dissimilarity. We design and train a Siamese deep neural network to find such an embedding, where the embedded descriptors are promoted to rearrange based on the geometric similarity. We found our approach can significantly enhance the performance of the conventional spectral descriptors for the non-isometric registration tasks, and outperforms recent state-of-the-art method reported in literature.

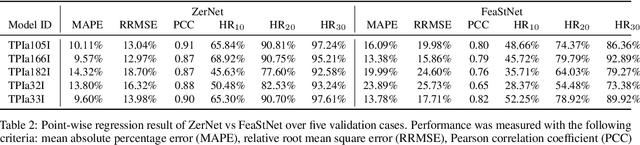
Wall Stress Estimation of Cerebral Aneurysm based on Zernike Convolutional Neural Networks

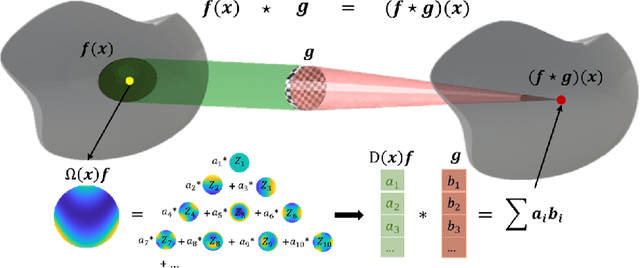
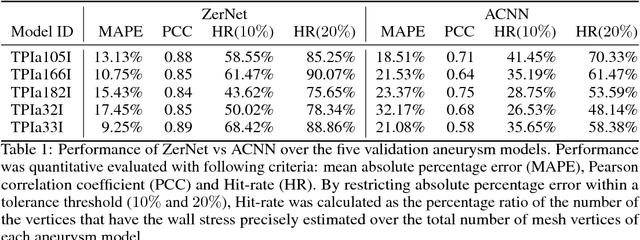
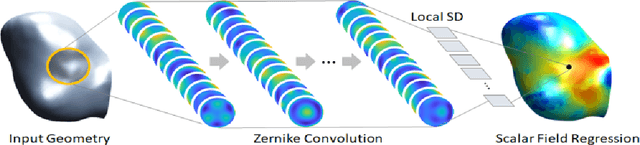
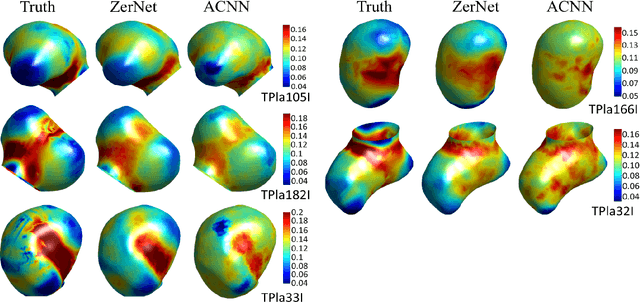
Convolutional neural networks (ConvNets) have demonstrated an exceptional capacity to discern visual patterns from digital images and signals. Unfortunately, such powerful ConvNets do not generalize well to arbitrary-shaped manifolds, where data representation does not fit into a tensor-like grid. Hence, many fields of science and engineering, where data points possess some manifold structure, cannot enjoy the full benefits of the recent advances in ConvNets. The aneurysm wall stress estimation problem introduced in this paper is one of many such problems. The problem is well-known to be of a paramount clinical importance, but yet, traditional ConvNets cannot be applied due to the manifold structure of the data, neither does the state-of-the-art geometric ConvNets perform well. Motivated by this, we propose a new geometric ConvNet method named ZerNet, which builds upon our novel mathematical generalization of convolution and pooling operations on manifolds. Our study shows that the ZerNet outperforms the other state-of-the-art geometric ConvNets in terms of accuracy.