Deep Spectral Descriptors: Learning the point-wise correspondence metric via Siamese deep neural networks
Paper and Code
Jun 25, 2018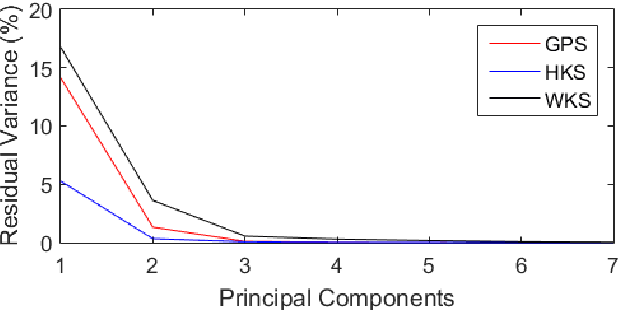

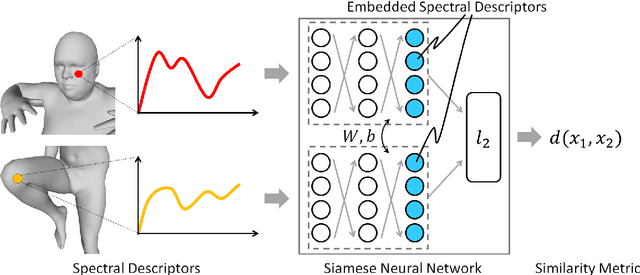

A robust and informative local shape descriptor plays an important role in mesh registration. In this regard, spectral descriptors that are based on the spectrum of the Laplace-Beltrami operator have gained a spotlight among the researchers for the last decade due to their desirable properties, such as isometry invariance. Despite such, however, spectral descriptors often fail to give a correct similarity measure for non-isometric cases where the metric distortion between the models is large. Hence, they are in general not suitable for the registration problems, except for the special cases when the models are near-isometry. In this paper, we investigate a way to develop shape descriptors for non-isometric registration tasks by embedding the spectral shape descriptors into a different metric space where the Euclidean distance between the elements directly indicates the geometric dissimilarity. We design and train a Siamese deep neural network to find such an embedding, where the embedded descriptors are promoted to rearrange based on the geometric similarity. We found our approach can significantly enhance the performance of the conventional spectral descriptors for the non-isometric registration tasks, and outperforms recent state-of-the-art method reported in literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge