Mutual Information Learned Regressor: an Information-theoretic Viewpoint of Training Regression Systems

As one of the central tasks in machine learning, regression finds lots of applications in different fields. An existing common practice for solving regression problems is the mean square error (MSE) minimization approach or its regularized variants which require prior knowledge about the models. Recently, Yi et al., proposed a mutual information based supervised learning framework where they introduced a label entropy regularization which does not require any prior knowledge. When applied to classification tasks and solved via a stochastic gradient descent (SGD) optimization algorithm, their approach achieved significant improvement over the commonly used cross entropy loss and its variants. However, they did not provide a theoretical convergence analysis of the SGD algorithm for the proposed formulation. Besides, applying the framework to regression tasks is nontrivial due to the potentially infinite support set of the label. In this paper, we investigate the regression under the mutual information based supervised learning framework. We first argue that the MSE minimization approach is equivalent to a conditional entropy learning problem, and then propose a mutual information learning formulation for solving regression problems by using a reparameterization technique. For the proposed formulation, we give the convergence analysis of the SGD algorithm for solving it in practice. Finally, we consider a multi-output regression data model where we derive the generalization performance lower bound in terms of the mutual information associated with the underlying data distribution. The result shows that the high dimensionality can be a bless instead of a curse, which is controlled by a threshold. We hope our work will serve as a good starting point for further research on the mutual information based regression.

What does AI see? Deep segmentation networks discover biomarkers for lung cancer survival

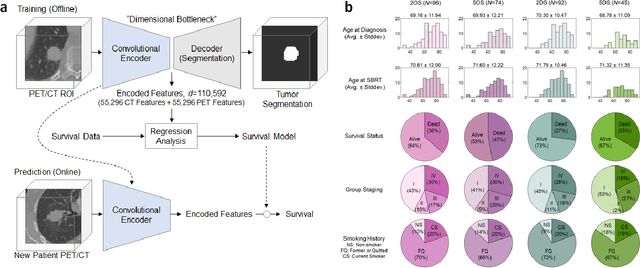
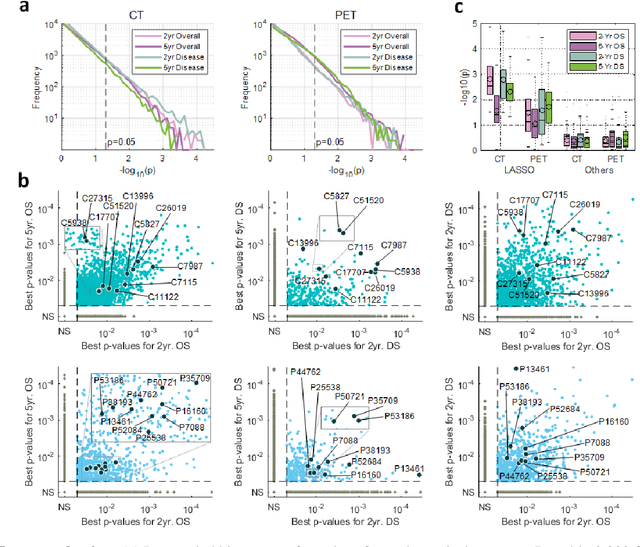
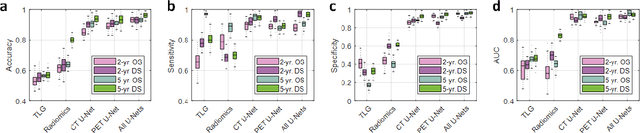
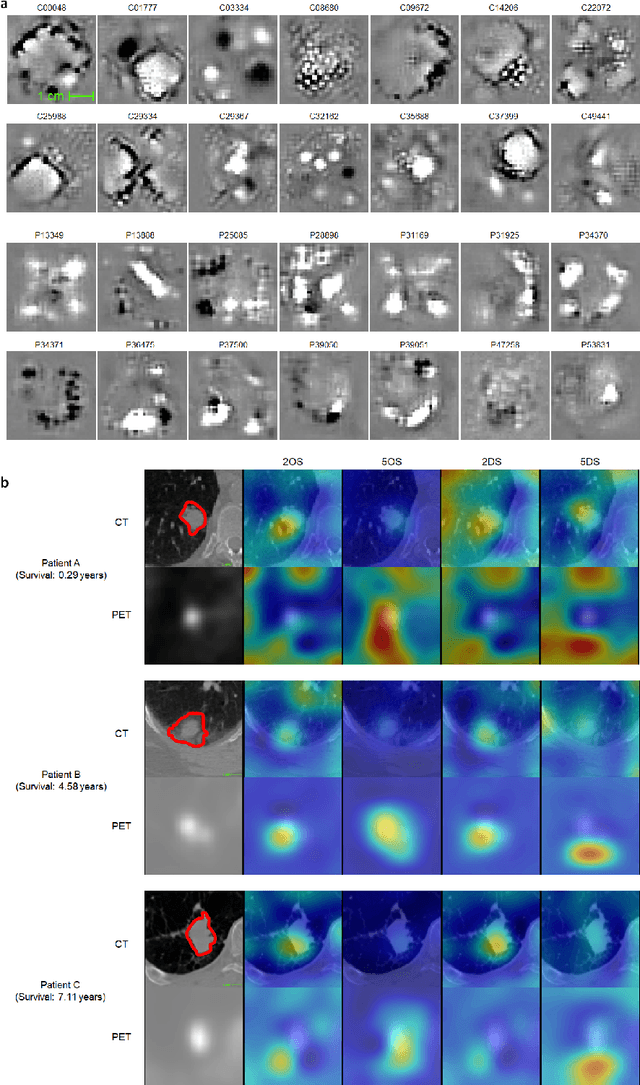
Non-small-cell lung cancer (NSCLC) represents approximately 80-85% of lung cancer diagnoses and is the leading cause of cancer-related death worldwide. Recent studies indicate that image-based radiomics features from positron emission tomography-computed tomography (PET/CT) images have predictive power on NSCLC outcomes. To this end, easily calculated functional features such as the maximum and the mean of standard uptake value (SUV) and total lesion glycolysis (TLG) are most commonly used for NSCLC prognostication, but their prognostic value remains controversial. Meanwhile, convolutional neural networks (CNN) are rapidly emerging as a new premise for cancer image analysis, with significantly enhanced predictive power compared to other hand-crafted radiomics features. Here we show that CNN trained to perform the tumor segmentation task, with no other information than physician contours, identify a rich set of survival-related image features with remarkable prognostic value. In a retrospective study on 96 NSCLC patients before stereotactic-body radiotherapy (SBRT), we found that the CNN segmentation algorithm (U-Net) trained for tumor segmentation in PET/CT images, contained features having strong correlation with 2- and 5-year overall and disease-specific survivals. The U-net algorithm has not seen any other clinical information (e.g. survival, age, smoking history) than the images and the corresponding tumor contours provided by physicians. Furthermore, through visualization of the U-Net, we also found convincing evidence that the regions of progression appear to match with the regions where the U-Net features identified patterns that predicted higher likelihood of death. We anticipate our findings will be a starting point for more sophisticated non-intrusive patient specific cancer prognosis determination.

Deep Spectral Descriptors: Learning the point-wise correspondence metric via Siamese deep neural networks

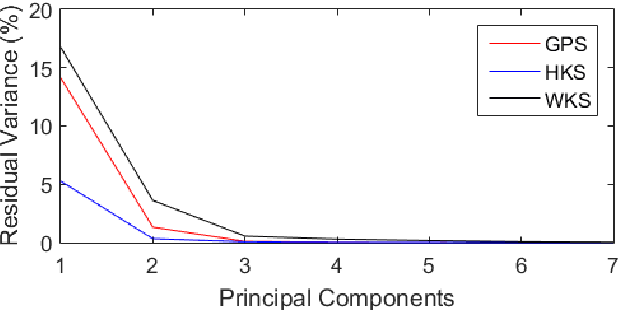
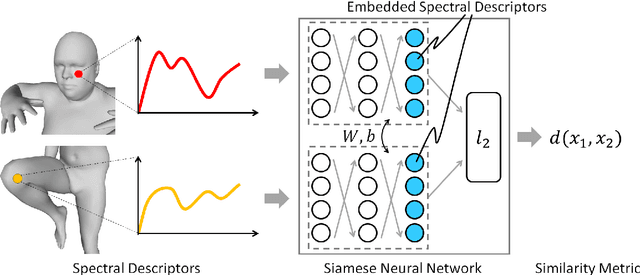
A robust and informative local shape descriptor plays an important role in mesh registration. In this regard, spectral descriptors that are based on the spectrum of the Laplace-Beltrami operator have gained a spotlight among the researchers for the last decade due to their desirable properties, such as isometry invariance. Despite such, however, spectral descriptors often fail to give a correct similarity measure for non-isometric cases where the metric distortion between the models is large. Hence, they are in general not suitable for the registration problems, except for the special cases when the models are near-isometry. In this paper, we investigate a way to develop shape descriptors for non-isometric registration tasks by embedding the spectral shape descriptors into a different metric space where the Euclidean distance between the elements directly indicates the geometric dissimilarity. We design and train a Siamese deep neural network to find such an embedding, where the embedded descriptors are promoted to rearrange based on the geometric similarity. We found our approach can significantly enhance the performance of the conventional spectral descriptors for the non-isometric registration tasks, and outperforms recent state-of-the-art method reported in literature.