ZerNet: Convolutional Neural Networks on Arbitrary Surfaces via Zernike Local Tangent Space Estimation

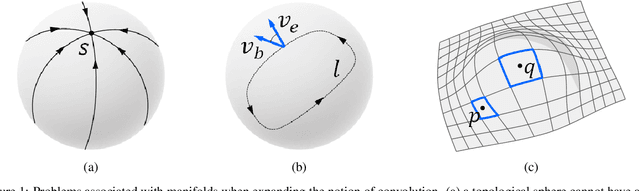
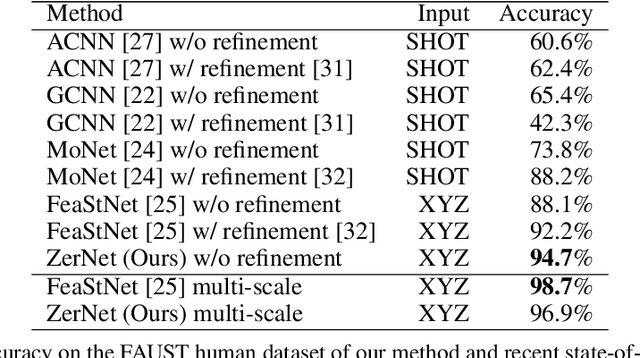
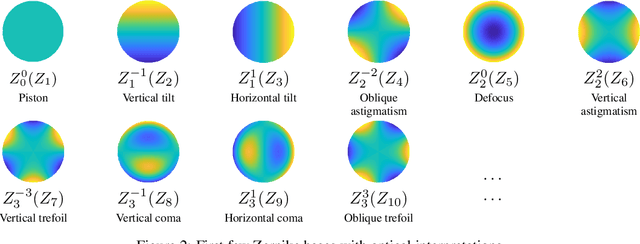
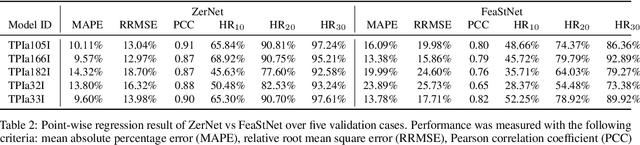
The research community has observed a massive success of convolutional neural networks (CNN) in visual recognition tasks. Such powerful CNNs, however, do not generalize well to arbitrary-shaped mainfold domains. Thus, still many visual recognition problems defined on arbitrary manifolds cannot benefit much from the success of CNNs, if at all. Technical difficulties hindering generalization of CNNs are rooted in the lack of a canonical grid-like representation, the notion of consistent orientation, and a compatible local topology across the domain. Unfortunately, except for a few pioneering works, only very little has been studied in this regard. To this end, in this paper, we propose a novel mathematical formulation to extend CNNs onto two-dimensional (2D) manifold domains. More specifically, we approximate a tensor field defined over a manifold using orthogonal basis functions, called Zernike polynomials, on local tangent spaces. We prove that the convolution of two functions can be represented as a simple dot product between Zernike polynomial coefficients. We also prove that a rotation of a convolution kernel equates to a 2 by 2 rotation matrix applied to Zernike polynomial coefficients, which can be critical in manifold domains. As such, the key contribution of this work resides in a concise but rigorous mathematical generalization of the CNN building blocks. Furthermore, comparative to the other state-of-the-art methods, our method demonstrates substantially better performance on both classification and regression tasks.