Wall Stress Estimation of Cerebral Aneurysm based on Zernike Convolutional Neural Networks
Paper and Code
Jun 20, 2018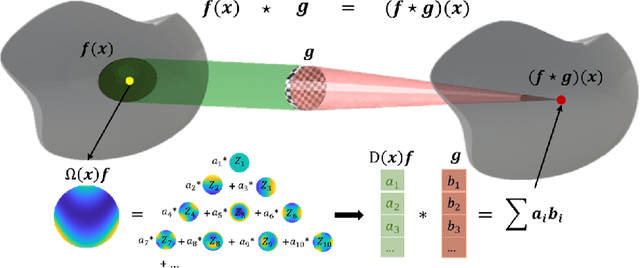
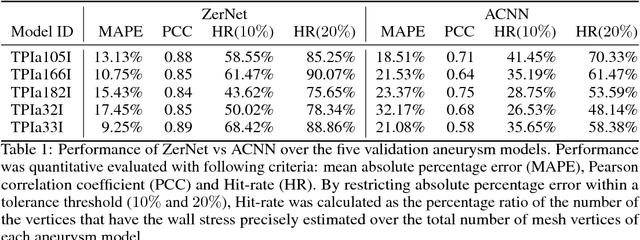
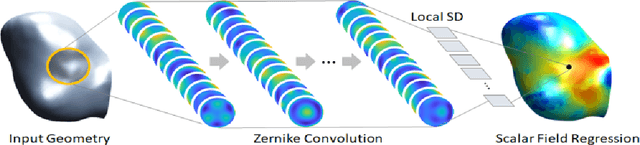
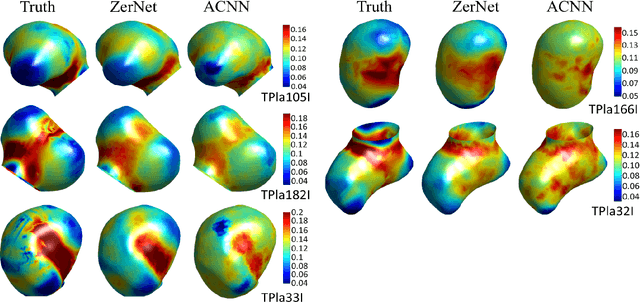
Convolutional neural networks (ConvNets) have demonstrated an exceptional capacity to discern visual patterns from digital images and signals. Unfortunately, such powerful ConvNets do not generalize well to arbitrary-shaped manifolds, where data representation does not fit into a tensor-like grid. Hence, many fields of science and engineering, where data points possess some manifold structure, cannot enjoy the full benefits of the recent advances in ConvNets. The aneurysm wall stress estimation problem introduced in this paper is one of many such problems. The problem is well-known to be of a paramount clinical importance, but yet, traditional ConvNets cannot be applied due to the manifold structure of the data, neither does the state-of-the-art geometric ConvNets perform well. Motivated by this, we propose a new geometric ConvNet method named ZerNet, which builds upon our novel mathematical generalization of convolution and pooling operations on manifolds. Our study shows that the ZerNet outperforms the other state-of-the-art geometric ConvNets in terms of accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge