Jean M. Vettel
Compact Convolutional Neural Networks for Classification of Asynchronous Steady-state Visual Evoked Potentials
Oct 09, 2018

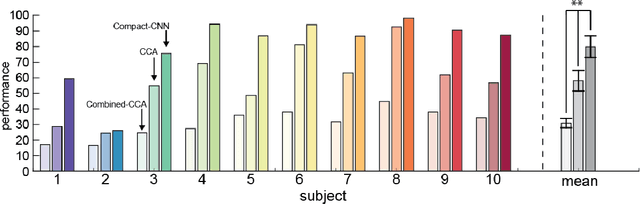
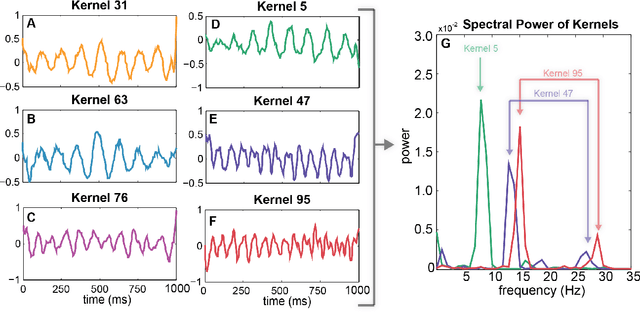
Abstract:Steady-State Visual Evoked Potentials (SSVEPs) are neural oscillations from the parietal and occipital regions of the brain that are evoked from flickering visual stimuli. SSVEPs are robust signals measurable in the electroencephalogram (EEG) and are commonly used in brain-computer interfaces (BCIs). However, methods for high-accuracy decoding of SSVEPs usually require hand-crafted approaches that leverage domain-specific knowledge of the stimulus signals, such as specific temporal frequencies in the visual stimuli and their relative spatial arrangement. When this knowledge is unavailable, such as when SSVEP signals are acquired asynchronously, such approaches tend to fail. In this paper, we show how a compact convolutional neural network (Compact-CNN), which only requires raw EEG signals for automatic feature extraction, can be used to decode signals from a 12-class SSVEP dataset without the need for any domain-specific knowledge or calibration data. We report across subject mean accuracy of approximately 80% (chance being 8.3%) and show this is substantially better than current state-of-the-art hand-crafted approaches using canonical correlation analysis (CCA) and Combined-CCA. Furthermore, we analyze our Compact-CNN to examine the underlying feature representation, discovering that the deep learner extracts additional phase and amplitude related features associated with the structure of the dataset. We discuss how our Compact-CNN shows promise for BCI applications that allow users to freely gaze/attend to any stimulus at any time (e.g., asynchronous BCI) as well as provides a method for analyzing SSVEP signals in a way that might augment our understanding about the basic processing in the visual cortex.
Local White Matter Architecture Defines Functional Brain Dynamics
Sep 16, 2018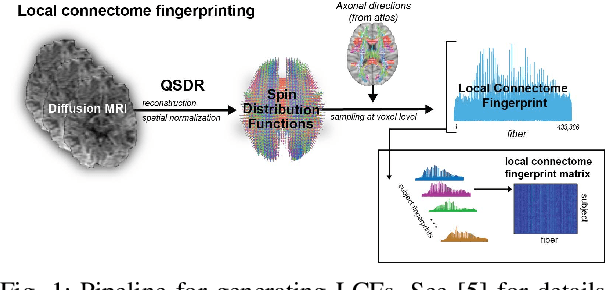
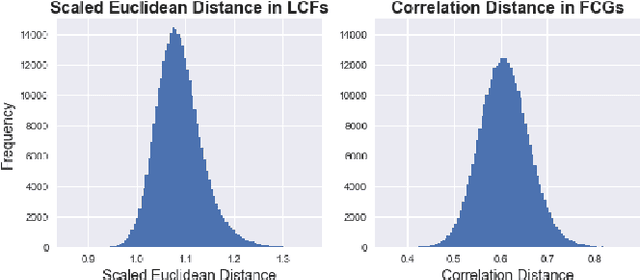
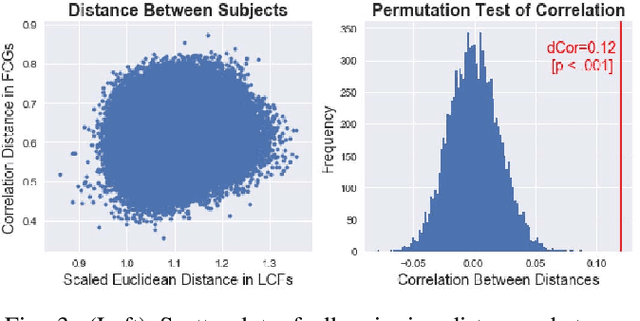
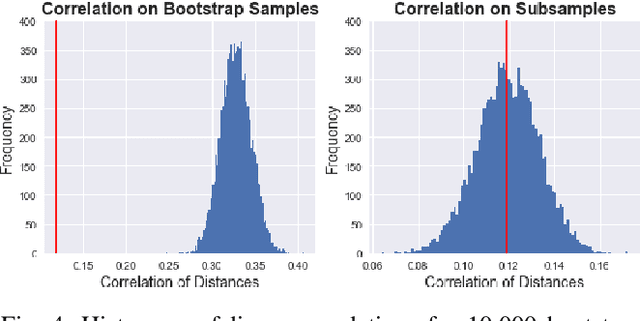
Abstract:Large bundles of myelinated axons, called white matter, anatomically connect disparate brain regions together and compose the structural core of the human connectome. We recently proposed a method of measuring the local integrity along the length of each white matter fascicle, termed the local connectome. If communication efficiency is fundamentally constrained by the integrity along the entire length of a white matter bundle, then variability in the functional dynamics of brain networks should be associated with variability in the local connectome. We test this prediction using two statistical approaches that are capable of handling the high dimensionality of data. First, by performing statistical inference on distance-based correlations, we show that similarity in the local connectome between individuals is significantly correlated with similarity in their patterns of functional connectivity. Second, by employing variable selection using sparse canonical correlation analysis and cross-validation, we show that segments of the local connectome are predictive of certain patterns of functional brain dynamics. These results are consistent with the hypothesis that structural variability along axon bundles constrains communication between disparate brain regions.
Riemannian-geometry-based modeling and clustering of network-wide non-stationary time series: The brain-network case
Jan 26, 2017
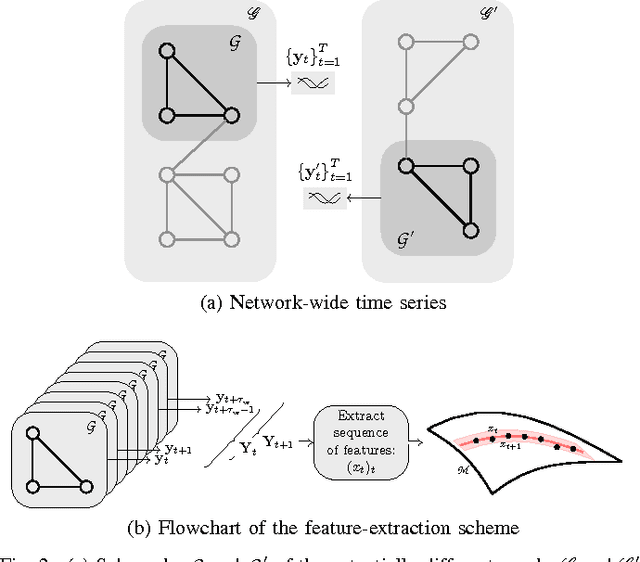
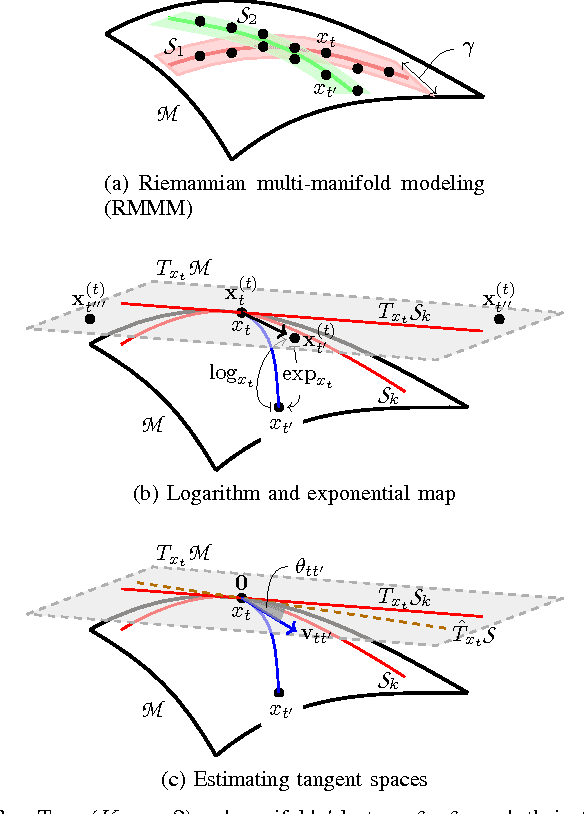
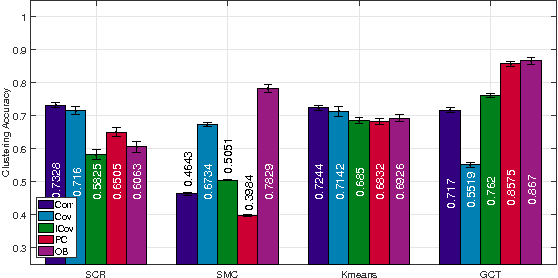
Abstract:This paper advocates Riemannian multi-manifold modeling in the context of network-wide non-stationary time-series analysis. Time-series data, collected sequentially over time and across a network, yield features which are viewed as points in or close to a union of multiple submanifolds of a Riemannian manifold, and distinguishing disparate time series amounts to clustering multiple Riemannian submanifolds. To support the claim that exploiting the latent Riemannian geometry behind many statistical features of time series is beneficial to learning from network data, this paper focuses on brain networks and puts forth two feature-generation schemes for network-wide dynamic time series. The first is motivated by Granger-causality arguments and uses an auto-regressive moving average model to map low-rank linear vector subspaces, spanned by column vectors of appropriately defined observability matrices, to points into the Grassmann manifold. The second utilizes (non-linear) dependencies among network nodes by introducing kernel-based partial correlations to generate points in the manifold of positive-definite matrices. Capitilizing on recently developed research on clustering Riemannian submanifolds, an algorithm is provided for distinguishing time series based on their geometrical properties, revealed within Riemannian feature spaces. Extensive numerical tests demonstrate that the proposed framework outperforms classical and state-of-the-art techniques in clustering brain-network states/structures hidden beneath synthetic fMRI time series and brain-activity signals generated from real brain-network structural connectivity matrices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge