Spatial Coherence of Oriented White Matter Microstructure: Applications to White Matter Regions Associated with Genetic Similarity

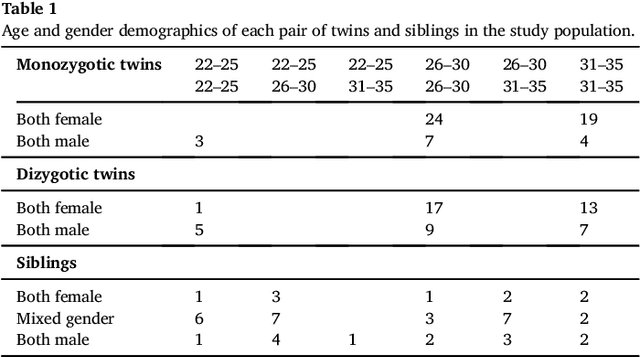
We present a method to discover differences between populations with respect to the spatial coherence of their oriented white matter microstructure in arbitrarily shaped white matter regions. This method is applied to diffusion MRI scans of a subset of the Human Connectome Project dataset: 57 pairs of monozygotic and 52 pairs of dizygotic twins. After controlling for morphological similarity between twins, we identify 3.7% of all white matter as being associated with genetic similarity (35.1k voxels, $p < 10^{-4}$, false discovery rate 1.5%), 75% of which spatially clusters into twenty-two contiguous white matter regions. Furthermore, we show that the orientation similarity within these regions generalizes to a subset of 47 pairs of non-twin siblings, and show that these siblings are on average as similar as dizygotic twins. The regions are located in deep white matter including the superior longitudinal fasciculus, the optic radiations, the middle cerebellar peduncle, the corticospinal tract, and within the anterior temporal lobe, as well as the cerebellum, brain stem, and amygdalae. These results extend previous work using undirected fractional anisotrophy for measuring putative heritable influences in white matter. Our multidirectional extension better accounts for crossing fiber connections within voxels. This bottom up approach has at its basis a novel measurement of coherence within neighboring voxel dyads between subjects, and avoids some of the fundamental ambiguities encountered with tractographic approaches to white matter analysis that estimate global connectivity.

Riemannian-geometry-based modeling and clustering of network-wide non-stationary time series: The brain-network case

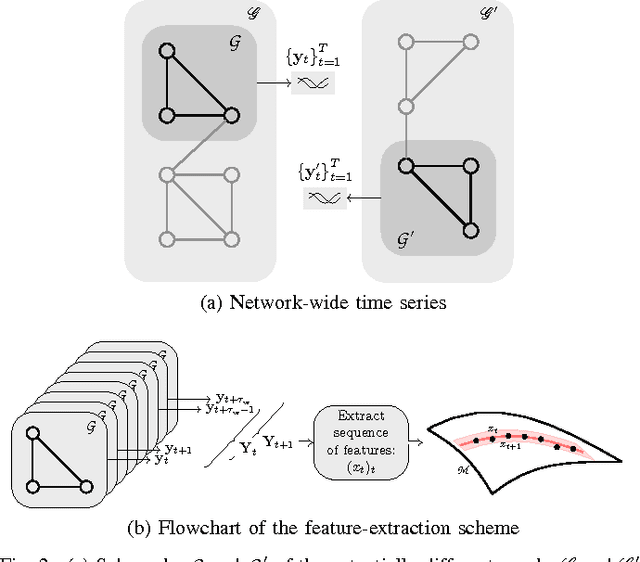
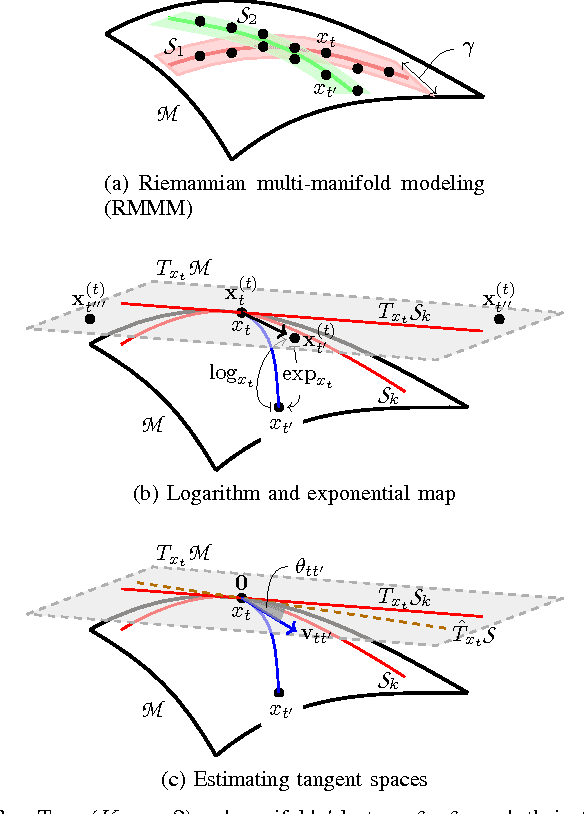
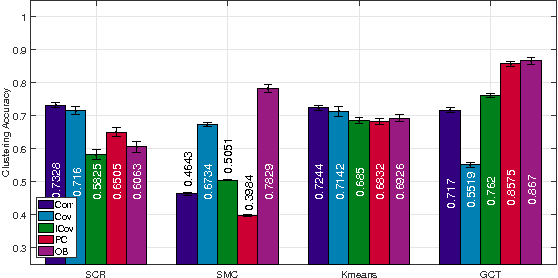
This paper advocates Riemannian multi-manifold modeling in the context of network-wide non-stationary time-series analysis. Time-series data, collected sequentially over time and across a network, yield features which are viewed as points in or close to a union of multiple submanifolds of a Riemannian manifold, and distinguishing disparate time series amounts to clustering multiple Riemannian submanifolds. To support the claim that exploiting the latent Riemannian geometry behind many statistical features of time series is beneficial to learning from network data, this paper focuses on brain networks and puts forth two feature-generation schemes for network-wide dynamic time series. The first is motivated by Granger-causality arguments and uses an auto-regressive moving average model to map low-rank linear vector subspaces, spanned by column vectors of appropriately defined observability matrices, to points into the Grassmann manifold. The second utilizes (non-linear) dependencies among network nodes by introducing kernel-based partial correlations to generate points in the manifold of positive-definite matrices. Capitilizing on recently developed research on clustering Riemannian submanifolds, an algorithm is provided for distinguishing time series based on their geometrical properties, revealed within Riemannian feature spaces. Extensive numerical tests demonstrate that the proposed framework outperforms classical and state-of-the-art techniques in clustering brain-network states/structures hidden beneath synthetic fMRI time series and brain-activity signals generated from real brain-network structural connectivity matrices.

On the geometric structure of fMRI searchlight-based information maps

Information mapping is a popular application of Multivoxel Pattern Analysis (MVPA) to fMRI. Information maps are constructed using the so called searchlight method, where the spherical multivoxel neighborhood of every voxel (i.e., a searchlight) in the brain is evaluated for the presence of task-relevant response patterns. Despite their widespread use, information maps present several challenges for interpretation. One such challenge has to do with inferring the size and shape of a multivoxel pattern from its signature on the information map. To address this issue, we formally examined the geometric basis of this mapping relationship. Based on geometric considerations, we show how and why small patterns (i.e., having smaller spatial extents) can produce a larger signature on the information map as compared to large patterns, independent of the size of the searchlight radius. Furthermore, we show that the number of informative searchlights over the brain increase as a function of searchlight radius, even in the complete absence of any multivariate response patterns. These properties are unrelated to the statistical capabilities of the pattern-analysis algorithms used but are obligatory geometric properties arising from using the searchlight procedure.