Network Clustering Via Kernel-ARMA Modeling and the Grassmannian The Brain-Network Case

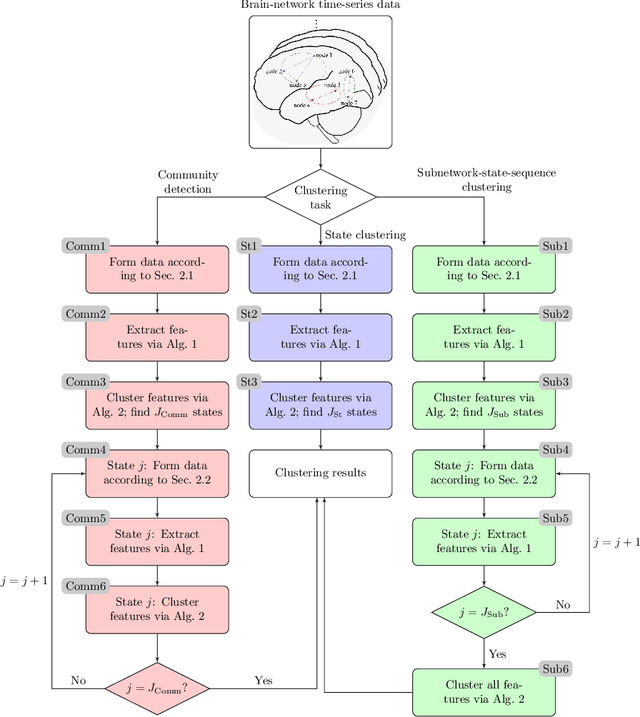
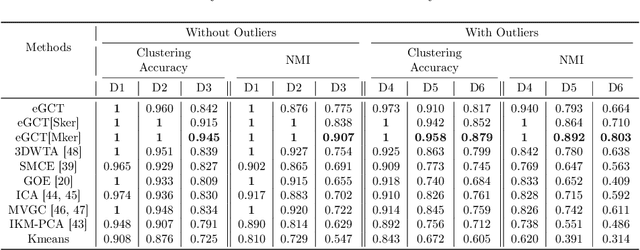
This paper introduces a clustering framework for networks with nodes annotated with time-series data. The framework addresses all types of network-clustering problems: State clustering, node clustering within states (a.k.a. topology identification or community detection), and even subnetwork-state-sequence identification/tracking. Via a bottom-up approach, features are first extracted from the raw nodal time-series data by kernel autoregressive-moving-average modeling to reveal non-linear dependencies and low-rank representations, and then mapped onto the Grassmann manifold (Grassmannian). All clustering tasks are performed by leveraging the underlying Riemannian geometry of the Grassmannian in a novel way. To validate the proposed framework, brain-network clustering is considered, where extensive numerical tests on synthetic and real functional magnetic resonance imaging (fMRI) data demonstrate that the advocated learning framework compares favorably versus several state-of-the-art clustering schemes.

Brain-Network Clustering via Kernel-ARMA Modeling and the Grassmannian

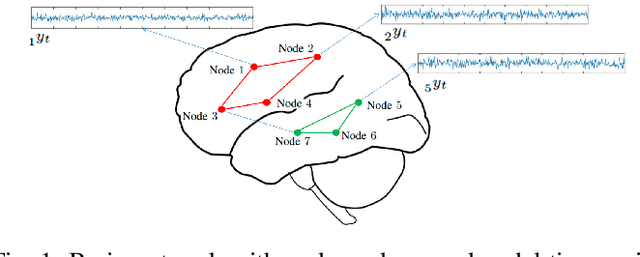
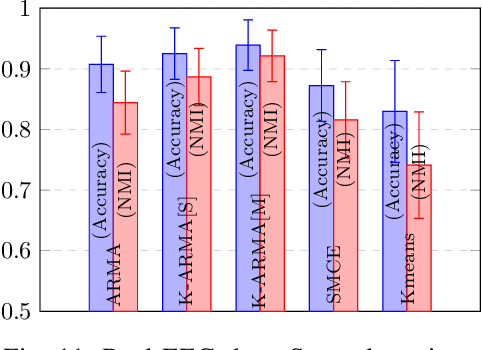
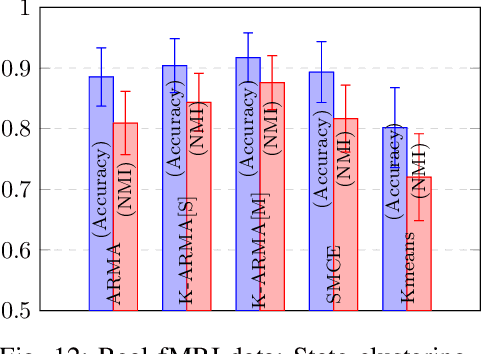
Recent advances in neuroscience and in the technology of functional magnetic resonance imaging (fMRI) and electro-encephalography (EEG) have propelled a growing interest in brain-network clustering via time-series analysis. Notwithstanding, most of the brain-network clustering methods revolve around state clustering and/or node clustering (a.k.a. community detection or topology inference) within states. This work answers first the need of capturing non-linear nodal dependencies by bringing forth a novel feature-extraction mechanism via kernel autoregressive-moving-average modeling. The extracted features are mapped to the Grassmann manifold (Grassmannian), which consists of all linear subspaces of a fixed rank. By virtue of the Riemannian geometry of the Grassmannian, a unifying clustering framework is offered to tackle all possible clustering problems in a network: Cluster multiple states, detect communities within states, and even identify/track subnetwork state sequences. The effectiveness of the proposed approach is underlined by extensive numerical tests on synthetic and real fMRI/EEG data which demonstrate that the advocated learning method compares favorably versus several state-of-the-art clustering schemes.

Riemannian-geometry-based modeling and clustering of network-wide non-stationary time series: The brain-network case

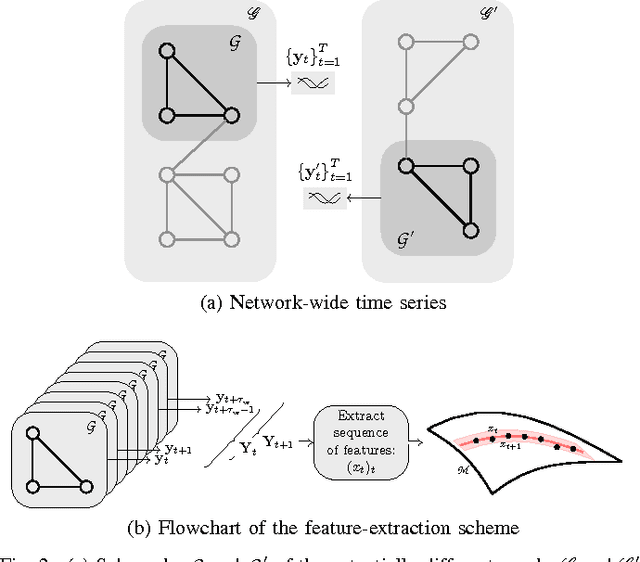
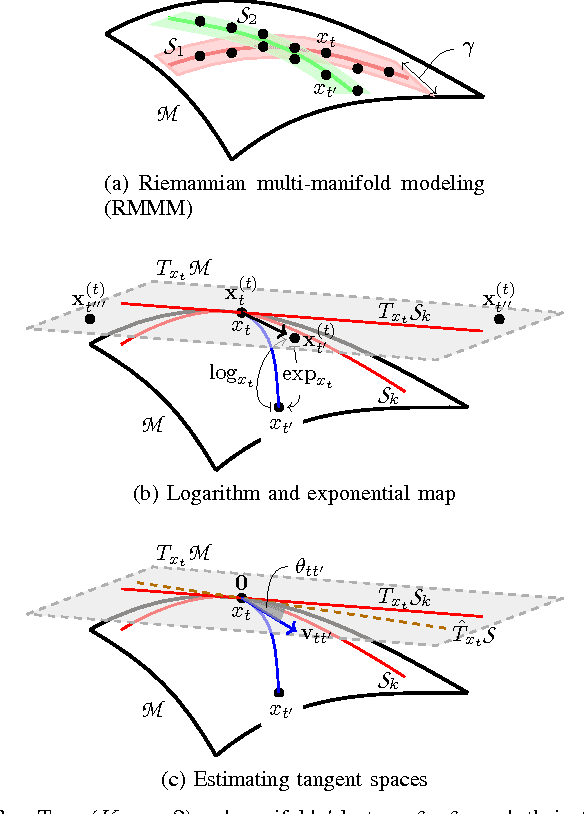
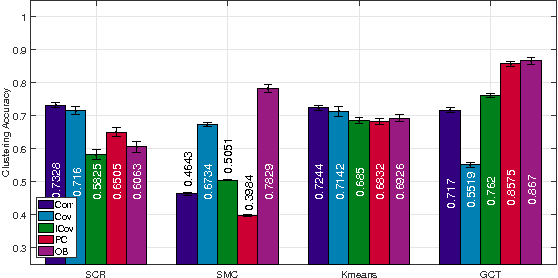
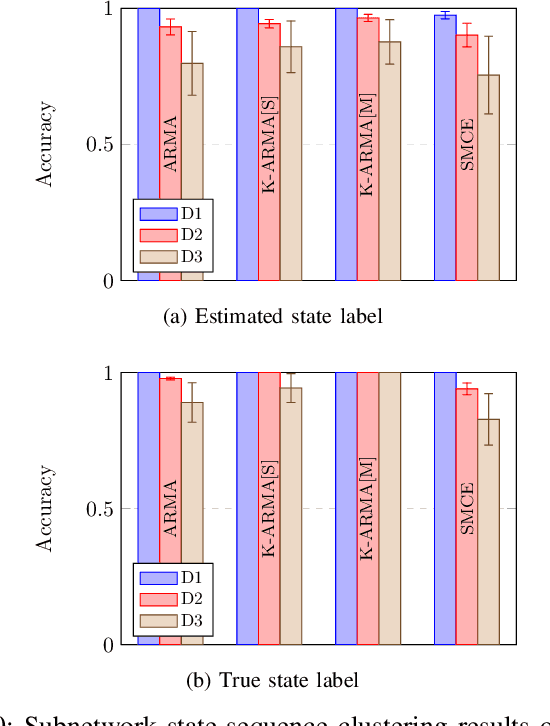
This paper advocates Riemannian multi-manifold modeling in the context of network-wide non-stationary time-series analysis. Time-series data, collected sequentially over time and across a network, yield features which are viewed as points in or close to a union of multiple submanifolds of a Riemannian manifold, and distinguishing disparate time series amounts to clustering multiple Riemannian submanifolds. To support the claim that exploiting the latent Riemannian geometry behind many statistical features of time series is beneficial to learning from network data, this paper focuses on brain networks and puts forth two feature-generation schemes for network-wide dynamic time series. The first is motivated by Granger-causality arguments and uses an auto-regressive moving average model to map low-rank linear vector subspaces, spanned by column vectors of appropriately defined observability matrices, to points into the Grassmann manifold. The second utilizes (non-linear) dependencies among network nodes by introducing kernel-based partial correlations to generate points in the manifold of positive-definite matrices. Capitilizing on recently developed research on clustering Riemannian submanifolds, an algorithm is provided for distinguishing time series based on their geometrical properties, revealed within Riemannian feature spaces. Extensive numerical tests demonstrate that the proposed framework outperforms classical and state-of-the-art techniques in clustering brain-network states/structures hidden beneath synthetic fMRI time series and brain-activity signals generated from real brain-network structural connectivity matrices.